2. Benchmark solution#
2.1. Modeling A#
This case models a mass that bounces off an elastic surface (modeling A)
2.1.1. Benchmark results#
The mass is released with an initial speed \({V}_{0}\) (configuration a), as long as it has not touched the ground, it only experiences gravity. When it touches the elastic ground, it is subjected, in addition to gravity, to a force of the type \(k\mathrm{.}\mathrm{\delta }x\) (configuration b). Once the rebound is over, it is only subjected to gravity (configuration a) with an initial speed \({V}_{1}\).
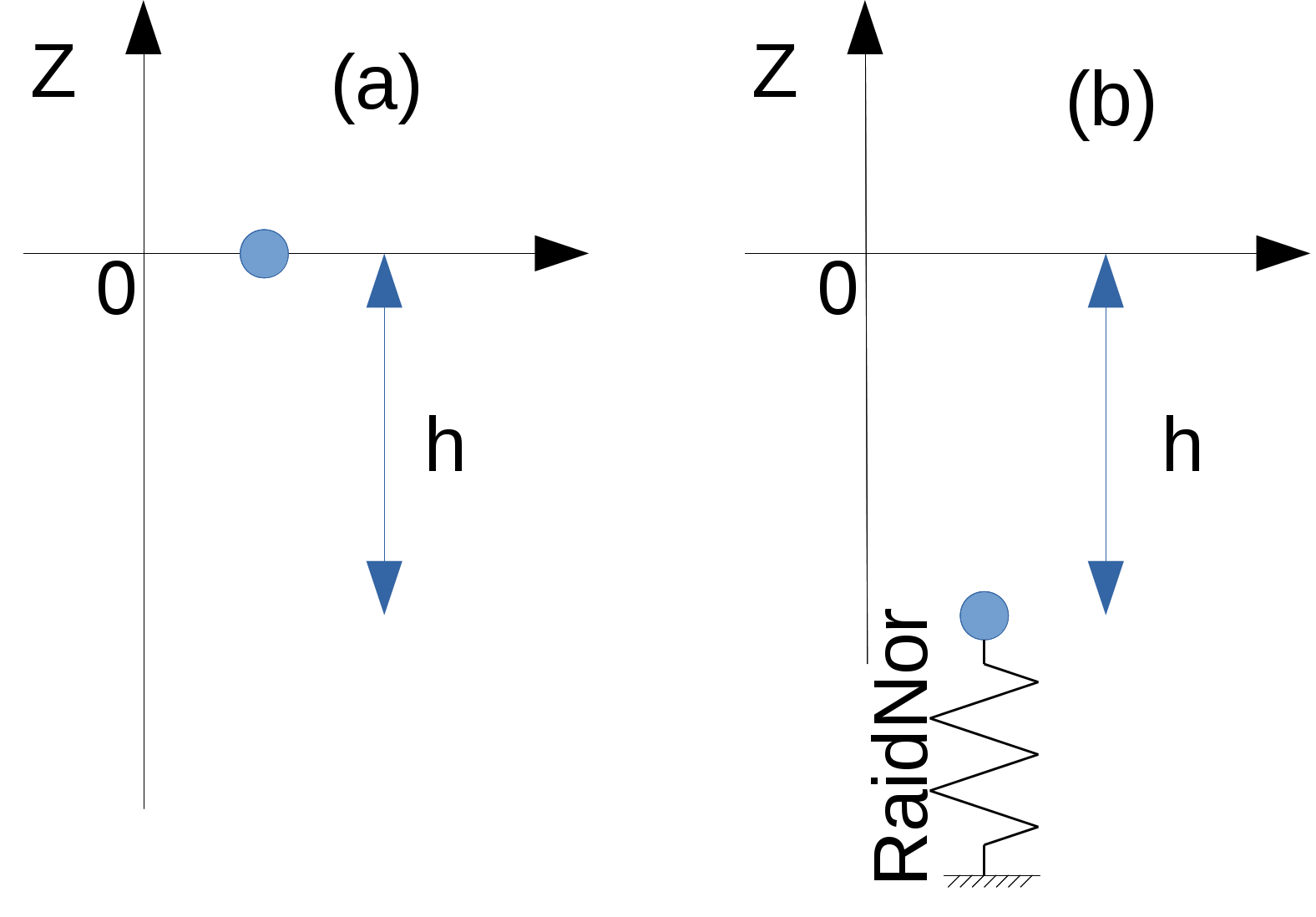
Table 2.1.1-1 : Behavioral model
Equation during free fall (configuration a):
Equation during rebound (configuration b):
: label: eq-4
mmathrm {.} ddot {x} =-mmathrm {.} g+kmathrm {.} (h-z)
And, therefore:
: label: eq-5
x= {C} _ {1}mathrm {sin} (wmathrm {.} stackrel {~} {t}) + {C} _ {2}mathrm {cos} (wmathrm {.} stackrel {~} {t}) + (h-g/ {w} ^ {2})
The two constants are valid:
2.2. B modeling#
This case models a mass that bounces off an absorbent surface.
2.2.1. Benchmark results#
The mass is released with an initial speed \({V}_{0}\) (configuration a), as long as it has not touched the surface, it only experiences gravity. When it touches the absorbent surface, in addition to gravity, it is subjected to a force of the \(k\mathrm{.}\mathrm{\delta }x+c\mathrm{.}\dot{x}\) type (configuration c). Once the rebound is over, it is only subjected to gravity (configuration a) with an initial speed \({V}_{1}\).
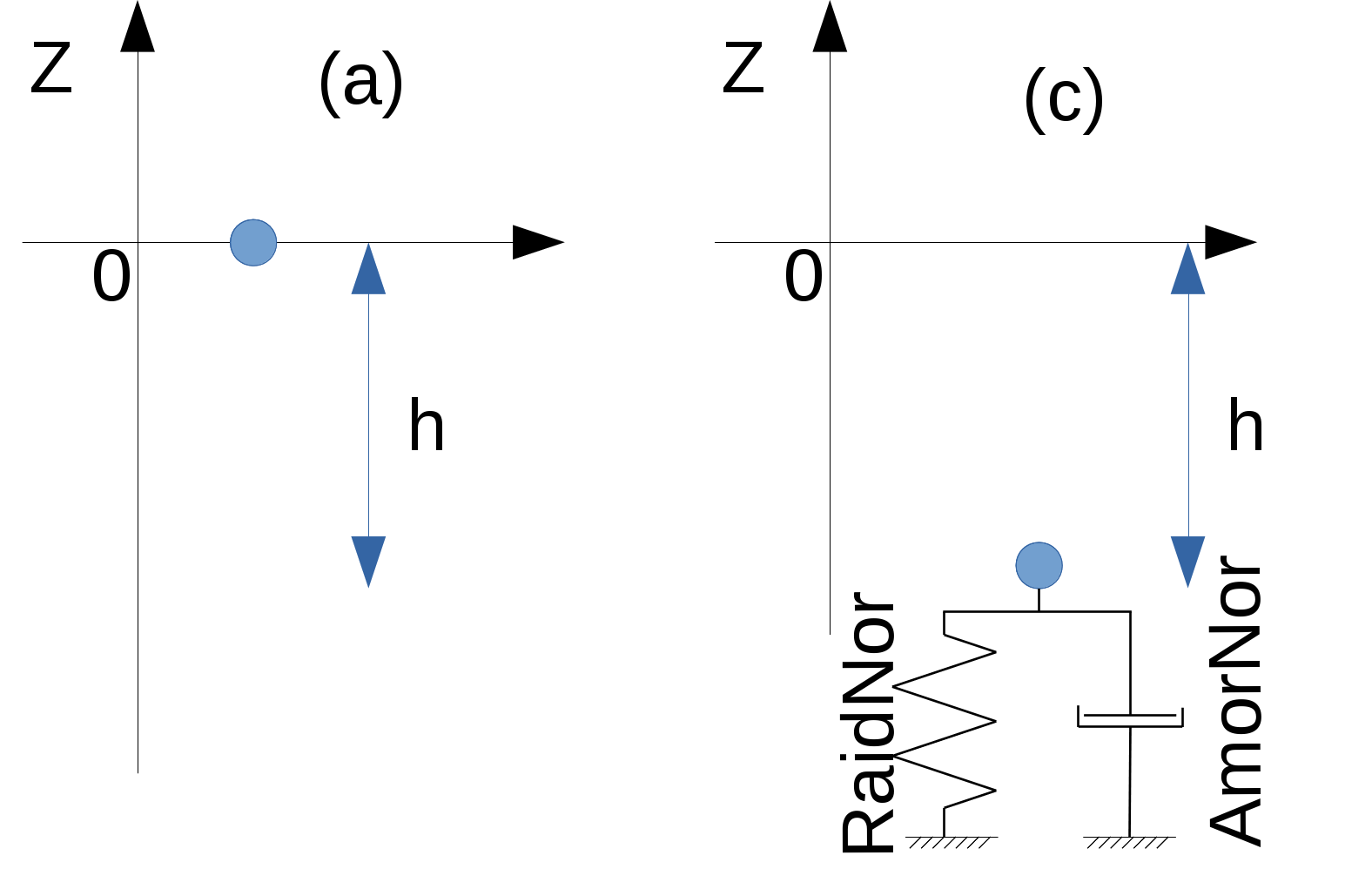
Table 2.2.1-1 :: ** Behavioral model
Equation during free fall (configuration a)
Equation during rebound (configuration c):
2.2.2. Uncertainty about solutions#
No uncertainty (analytical solution).