1. Reference issues

1.1. Geometry of the « rectangle » crack

Consider a cube with a side of \(1m\). This cube has a rectangle-shaped crack with rounded corners. The crack is located in the plane of normal \(y\) halfway between the front and back side of the cube (see). The crack is actually a half-rectangle. The length of the complete rectangle is \(\mathrm{2a}\) and the width is \(\mathrm{2b}\). In addition, the corners of the rectangle are rounded, with a radius \(r\). So the center of the full rectangle is the coordinate point \((\mathrm{0,5};\mathrm{0,5};1)\). The center of the coordinate system is point \(\mathrm{P4}\). In the following, we’ll take \(a=\mathrm{0,3}\), \(b=\mathrm{0,15}\) and \(r=\mathrm{0,05}\).

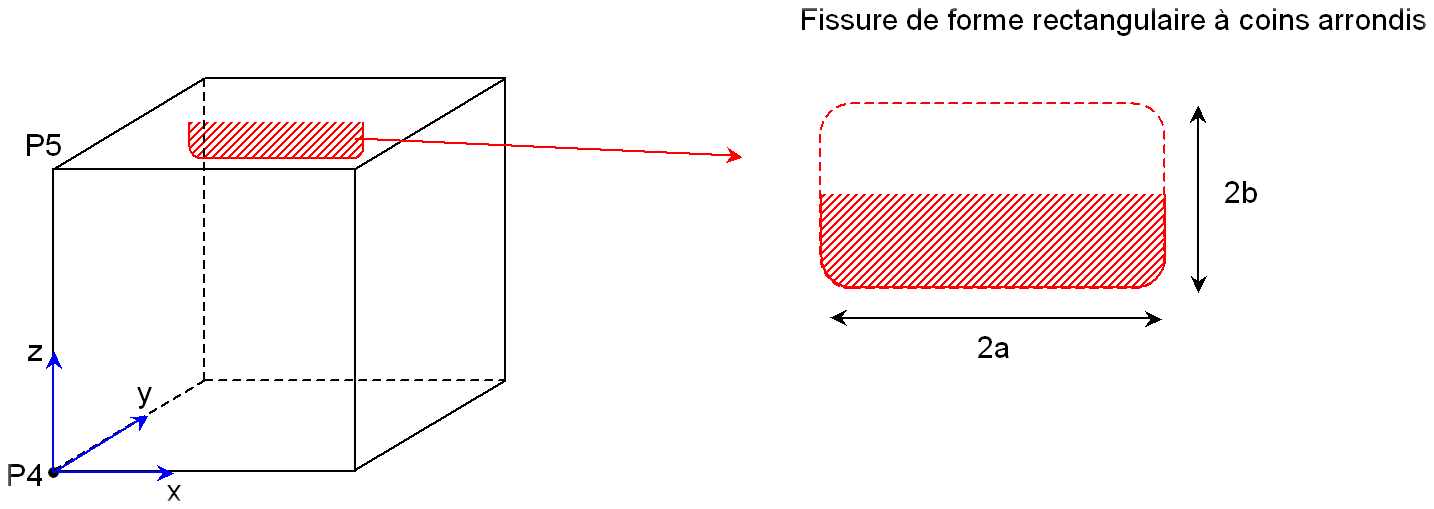
Figure 1.1-1 : diagram of the cube cracked by the « rectangle » crack

1.2. Geometry of the « cylinder » crack

We consider the same cube as before, but including a crack in the form of a cylinder. The cylinder axis is parallel to the \(y\) axis and passes through the point \(C\) with coordinates \((1;\mathrm{0,5};1)\). The radius of the cylinder is \(r\mathrm{=}\mathrm{0,5}\). The crack front is therefore a quarter of a circle. The lips of the crack are located in half-space \(y\mathrm{\le }\mathrm{0,5}\) (see).

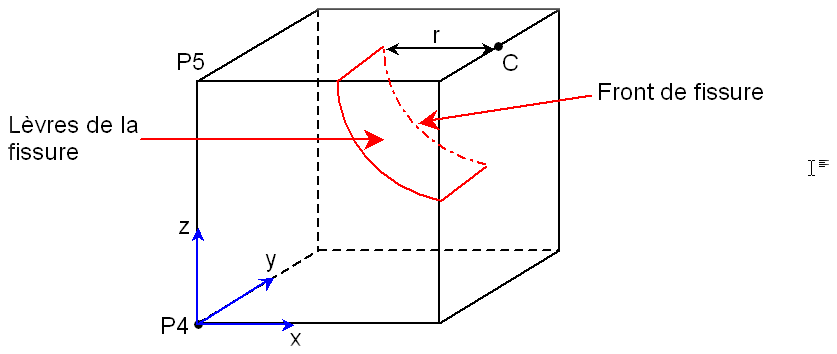
Figure 1.2-1: diagram of the cube cracked by the « cylinder » crack