3. Modeling A#
The crack bottom is closed. We calculate \(G\).
3.1. Characteristics of modeling#
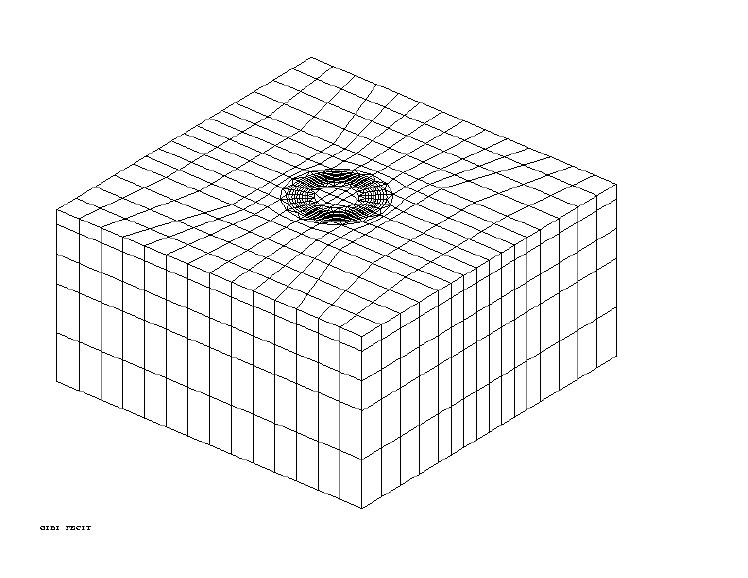
The advantage of this modeling is to represent the entire crack background, which is a closed curve, without taking advantage of the symmetries of the problem.
Only traction loading is taken into account.
3.2. Characteristics of the mesh#
Number of knots: 11114
Number of meshes and type: 2432 PENTA15
The middle nodes of the edges of the elements touching the bottom of the crack are moved to a quarter of these edges.
3.3. note#
The keyword SYME is used in the CALC_G operator to automatically multiply by two the energy restoration rate calculated on a single lip of the crack, when the FOND_FISS operand is absent. When FOND_FISS is present, symmetry information is retrieved directly from the fond_fiss concept created via DEFI_FOND_FISS.
The principle is the same for POST_K1_K2_K3. The indication of the symmetry induces the calculation of the stress intensity factors and the energy restoration rate G_ IRWIN by interpolation of the movements of a single lip of the crack. Moving the middle nodes of the edges of the elements touching the bottom of the crack to a quarter of these edges would improve the accuracy of the calculation.
3.4. Tested sizes and results#
Identification |
Reference |
Reference type |
\(\text{\%}\) tolerance |
G local Node \(N403\) - Discretization LINEAIRE, R_ INF and R_ SUP |
11.586 |
|
3.0 |
G local Node \(N2862\) - Discretization LINEAIRE, R_ INF and R_ SUP |
11.586 |
|
2.0 |
G local Node \(N375\) - Discretization LINEAIRE, R_ INF and R_ SUP |
11.586 |
|
3.0 |
G local Node \(N292\) - Discretization LINEAIRE, R_ INF and R_ SUP |
11.586 |
|
2,4 |
\(\mathit{max}(G\mathit{local})\) - Discretization LINEAIRE, R_ INF R_ SUP |
11.59 |
|
2.5 |
\(\mathit{min}(G\mathit{local})\) - Discretization LINEAIRE, R_ INF R_ SUP |
11.59 |
|
2.0 |
G local point \(1\) Discretization LINEAIRE/NB_POINT_FOND =33, R_ INF and R_ SUP |
11.586 |
|
1.0 |
G local point \(13\) Discretization LINEAIRE/NB_POINT_FOND =33, R_ INF and R_ SUP |
11.586 |
|
1.0 |
G local point \(21\) Discretization LINEAIRE/NB_POINT_FOND =33, R_ INF and R_ SUP |
11.586 |
|
1.0 |
G local point \(33\) Discretization LINEAIRE/NB_POINT_FOND =33, R_ INF and R_ SUP |
11.586 |
|
1.0 |
G local Node \(N403\) - Discretization LINEAIRE, NB_COUCHE_INF and NB_COUCHE_SUP |
11.586 |
|
3.0 |
G local Node \(N2862\) - Discretization LINEAIRE, NB_COUCHE_INF and NB_COUCHE_SUP |
11.586 |
|
2.0 |
G local Node \(N375\) - Discretization LINEAIRE, NB_COUCHE_INF and NB_COUCHE_SUP |
11.586 |
|
3.0 |
G local Node \(N292\) - Discretization LINEAIRE, NB_COUCHE_INF and NB_COUCHE_SUP |
11.586 |
|
2,4 |
\(\mathit{max}(G\mathit{local})\) - Discretization LINEAIRE, NB_COUCHE_INF and NB_COUCHE_SUP |
11.59 |
|
2.5 |
\(\mathit{min}(G\mathit{local})\) - Discretization LINEAIRE, NB_COUCHE_INF and NB_COUCHE_SUP |
11.59 |
|
2.0 |
G local point \(1\) Discretization LINEAIRE/NB_POINT_FOND =33/=33, NB_COUCHE_INF and NB_COUCHE_SUP |
11.586 |
|
1.0 |
G local point \(13\) Discretization LINEAIRE/NB_POINT_FOND =33/=33, NB_COUCHE_INF and NB_COUCHE_SUP |
11.586 |
|
1.0 |
G local point \(21\) Discretization LINEAIRE/NB_POINT_FOND =33/=33, NB_COUCHE_INF and NB_COUCHE_SUP |
11.586 |
|
1.0 |
G local point \(33\) Discretization LINEAIRE/NB_POINT_FOND =33/=33, NB_COUCHE_INF and NB_COUCHE_SUP |
11.586 |
|
1.0 |