1. Reference problem#

1.1. Geometry#

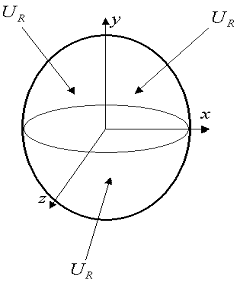
_images/10000000000000F90000011B9305DA76C4C14512.png

Figure 1.1-a

The geometry of the structure is a ball of unit radius for the analytical solution.

1.2. Material properties#

In the context of second gradient media, it is necessary to define material properties for the parts associated with the first and second gradients of the displacement field. The properties of the material have no physical relevance but have been established to simplify analytical applications.

      • Young’s module: \(\text{E}\mathrm{=}1\text{Pa}\);

      • Poisson’s ratio: \(\nu =0\);

      • Second gradient stiffness module: \({a}_{1}\mathrm{=}0.25{\text{Pa.m}}^{2}\).

1.3. Boundary conditions and loads#

For reasons of numerical simplifications, we only consider one eighth of the ball by symmetry:

  • \(\mathit{DX}\mathrm{=}0\) on the GROUP_MA “SYME_X”

  • \(\mathit{DY}\mathrm{=}0\) on the GROUP_MA “SYME_Y”

  • \(\mathit{DZ}\mathrm{=}0\) on the GROUP_MA “SYME_Z”

For reasons of numerical simplifications, we do not model the ball but the inscribed cube of this ball for the application of boundary conditions. In frame \(X\mathrm{=}(x,y,z)\), we thus apply:

  • \({U}_{R}(X)\mathrm{=}(\frac{{r}^{4}}{7}\mathrm{-}\frac{1}{3})X\) for DX components, DYet DZdu GROUP_MA “BORD_EXT” where \(r\) is the distance between the origin of the ball and the point with the coordinate \(X\).

  • \({G}_{R}(X)\mathrm{=}({r}^{4}\mathrm{-}1)\) for GONFdu GROUP_MA “BORD_EXT” components.

Finally, the following internal forces are applied in frame \(X\mathrm{=}(x,y,z)\):

\({F}_{I}(X)\mathrm{=}4(10\mathrm{-}{r}^{2})X\) for FX components, FYet FZdu GROUP_MA “BORD_EXT”