3. Modeling A#
3.1. Characteristics of modeling#
We use a POU_D_EM model.
the beam is modelled with 1 finite element and the section is discretized with 8 fibers. The reference axis is deliberately chosen different from the barycenter, offset by h/2 downwards, with the keyword COOR_AXE_POUTRE from DEFI_GEOM_FIBRE.
The section is « cut » into 8 fibers (Figure 2). The coordinates of the fiber centers and their areas are given in table 1.
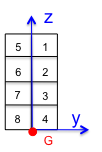
Figure 2: Dividing the section into 8 fibers
Fibers |
\({y}_{i}\) |
|
|
Fibers |
\({y}_{i}\) |
|
|
||
1 |
0.1 |
0.875 |
0.75 |
0.05 |
5 |
-0.1 |
0.875 |
0.05 |
|
2 |
0.1 |
0.625 |
0.05 |
0.05 |
6 |
-0.1 |
0.625 |
0.05 |
|
3 |
0.1 |
0.375 |
0.05 |
0.05 |
7 |
-0.1 |
0.375 |
0.05 |
|
4 |
0.1 |
0.125 |
0.05 |
0.05 |
8 |
-0.1 |
0.125 |
0.05 |
Table 1: Characteristics of fibers
3.2. Characteristics of the mesh#
The mesh contains 1 elements of type SEG2.
3.3. Tested sizes and results#
Numerical calculation of the quantities of the straight section gives:
\(S=0.4{m}^{2}\) \({A}_{G}=0.2{m}^{3}\) \({I}_{G}=0.13125{m}^{4}\) and \({I}_{{G}_{0}}=0.03125{m}^{4}\)
The arrow at the loaded end of the beam is: \(f=0.00035555m\)
At the level of embedding \(x=0\) we have the following values:
\(M=-{10}^{-6}\mathit{Nm}\) \({\chi }_{s}=0.00106666{m}^{-1}\) \({ϵ}_{s}=-0.00053333{m}^{-1}\)
At the level of the first Gauss point \(x=(1-\frac{1}{\sqrt{3}})/2=0.21132486540518503m\) we have the following values: \(M=-788675.13\mathit{Nm}\) \({\chi }_{s}=0.00084125{m}^{-1}\) \({ϵ}_{s}=-0.0004206{m}^{-1}\)
for fiber No. 1 (\(z=0.875m\)): \(ϵ=0.00031547\) and \(\sigma =9464101.6\mathit{Pa}\) and for fiber No. 4 to \(z=0.125m\) \(ϵ=-0.00031547\) and \(\sigma =-9464101.6\mathit{Pa}\)
Boom at the end of the beam (DEPL):
Point |
Component |
Reference Value |
Tolerance |
APPUI |
DZ |
\(-3.5555555555555E-4\) |
|
Generalized deformations during embedding (DEGE_ELNO):
Mesh |
Knot |
Component |
Reference Value |
Tolerance |
M1 |
N1 |
KY |
\(1.066666666666667E-3\) |
|
M1 |
N1 |
|
|
|
Deformations and stresses in fibers (EPSI_ELGA and SIEF_ELGA):
Mesh |
Point |
Sub-Point |
Sub-Point |
Component |
Reference Value |
Tolerance |
M1 |
1 |
1 |
|
|
|
|
M1 |
1 |
1 |
|
|
|
|
M1 |
1 |
4 |
|
|
|
|
M1 |
1 |
4 |
|
|
|