1. Reference problem

1.1. Geometry

Consider a square with a side of \(1m\), shown below:

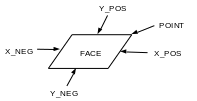
1.2. Material properties

The square has anisotropic membrane behavior, characterized by the following coefficients (the coefficients not mentioned are zero):

\(\mathrm{\{}\begin{array}{c}{M}_{\mathit{LLLL}}\mathrm{=}3\\ {M}_{\mathit{TTTT}}\mathrm{=}3\\ {M}_{\mathit{LLTT}}\mathrm{=}1\\ {M}_{\mathit{LTLT}}\mathrm{=}2\end{array}\)

These coefficients are defined in a coordinate system rotated by 90° around the \((\mathit{Oz})\) axis.

1.3. Boundary conditions and loads

Two calculations are carried out, corresponding to a tensile stress and a shear load of the membrane. The corresponding limit conditions are shown below:

• Traction solicitation

\(\mathrm{\{}\begin{array}{c}{u}_{Z}\mathrm{=}0\text{sur}\text{FACE}\\ {u}_{X}\mathrm{=}0\text{sur}\text{X\_NEG}\\ {u}_{Y}\mathrm{=}0\text{sur}\text{Y\_NEG}\\ {F}_{X}\mathrm{=}1\text{sur}\text{X\_POS}\end{array}\)

• Shear load

\(\mathrm{\{}\begin{array}{c}{u}_{Z}\mathrm{=}0\text{sur}\text{FACE}\\ {u}_{Y}\mathrm{=}0\text{sur}\text{X\_NEG}\\ {u}_{X}\mathrm{=}0\text{sur}\text{Y\_NEG}\\ {u}_{X}\mathrm{=}{u}_{Y}\text{sur}\text{POINT}\\ {F}_{Y}\mathrm{=}1\text{sur}\text{X\_POS}\\ {F}_{X}\mathrm{=}1\text{sur}\text{Y\_POS}\end{array}\)