2. Benchmark solution#
2.1. Calculation method#
The densities of longitudinal steels are calculated according to the Capra and Maury method, for the directions \(\text{X}\) and \(\text{Y}\) of each element and according to the 2 faces, \(\text{I}\) (Lower) and \(\text{S}\) (Upper), defined by their position according to the elementary \(\text{Z}\) normal. The transverse steel density is also calculated as described in the article entitled « Automatic calculation of the optimal reinforcement of reinforced concrete plates or shells » by Alain CAPRA and Jean-Francis MAURY.
2.2. Benchmark results#
The various results are published in the article by Capra and Maury in the form of graphs (for a quarter of a model only) are:
the deformation of the tank,
the iso-moments \(\text{Mxx}\) and \(\text{Myy}\),
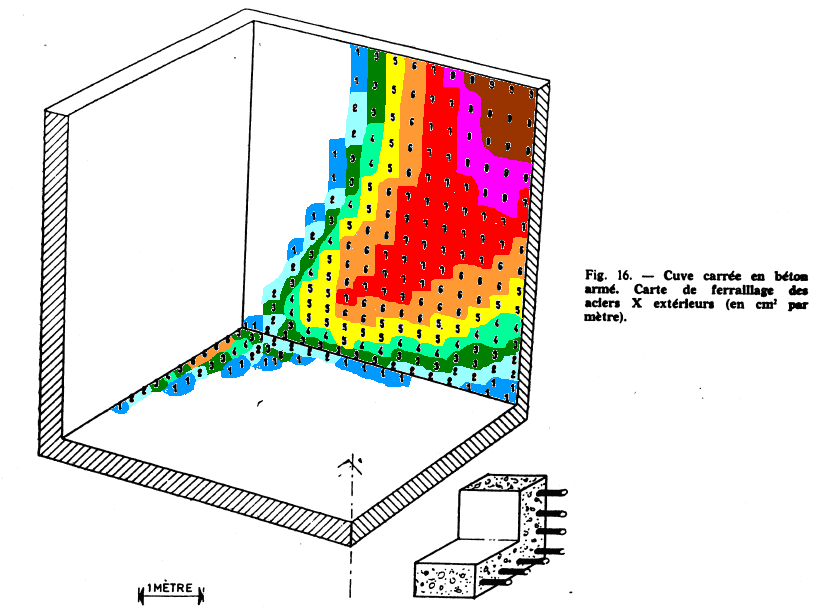
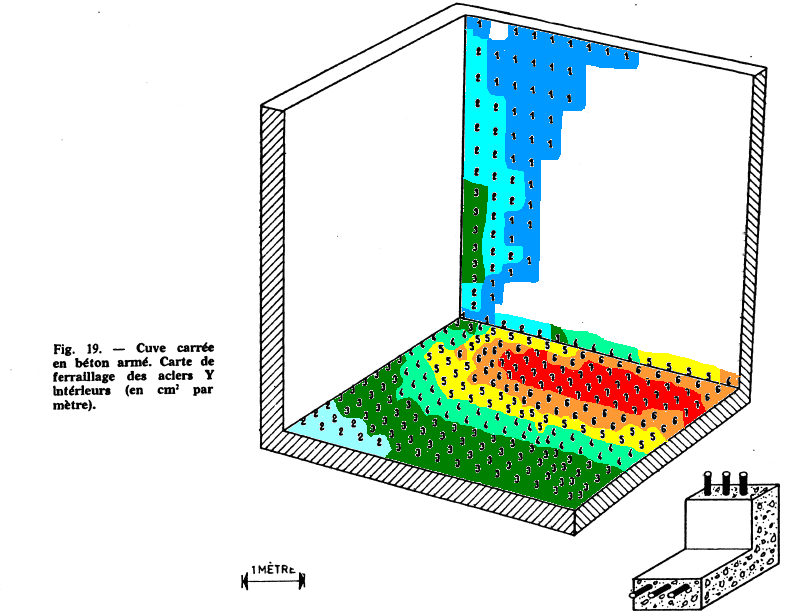
reinforcement densities in the directions \(\text{X}\) and \(\text{Y}\) at the top and bottom.
Below is the excerpt from the article for the deformed and the moments \(\text{Mx}\), \(\text{My}\).
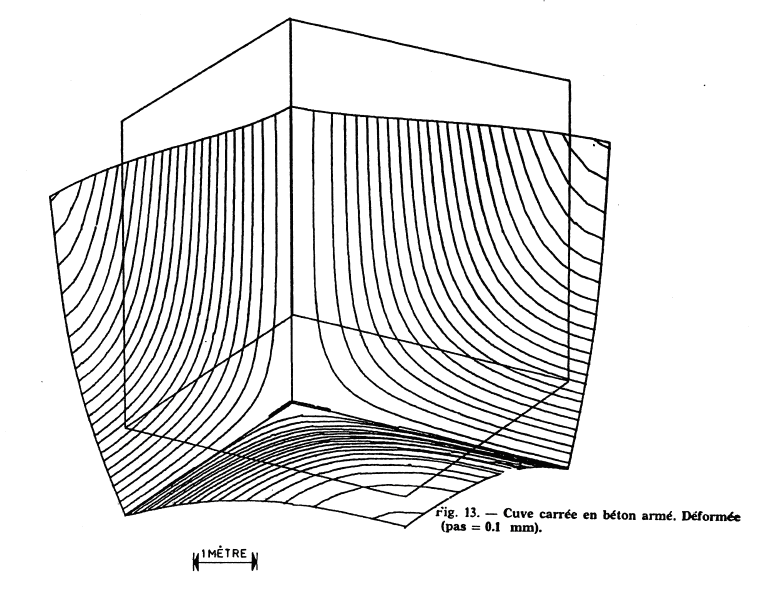
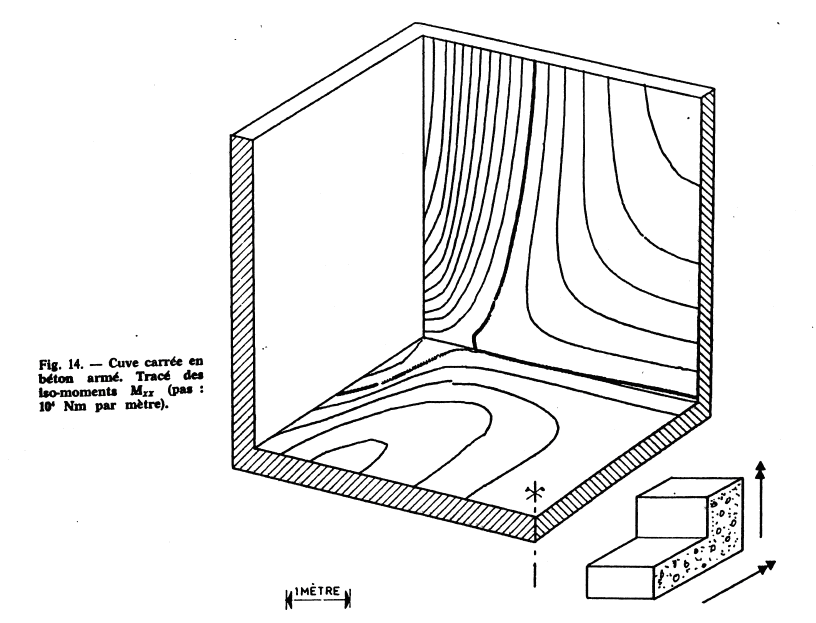
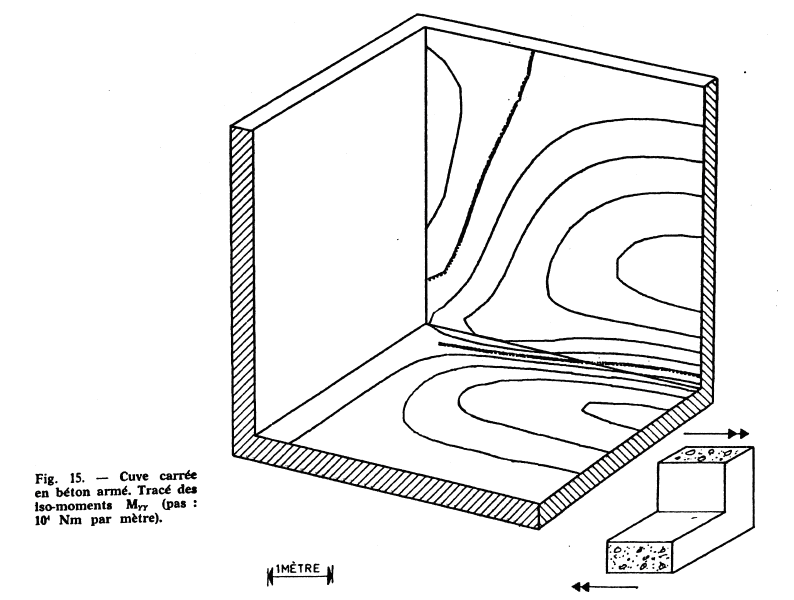
Below is the excerpt from the article for reinforcement densities. For better readability, colors have been associated with the various reinforcement density values.


2.3. Bibliographical references#
[1] Annals of the Technical Institute of Building and Public Works N° 367 December 1978 - Series: INFORMATIQUE APPLIQUEE - Article entitled « Automatic calculation of the optimal reinforcement of reinforced concrete plates or shells » by Alain CAPRA and Jean-Francis MAURY.