1. Reference problem#

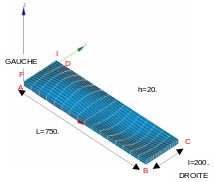
1.1. Geometry#
Dot |
\(X(\mathit{mm})\) |
|
|
|
\(A\) |
0 |
0 |
0 |
|
\(B\) |
750 |
0 |
10 |
|
\(C\) |
750 |
200 |
10 |
|
\(D\) |
0 |
200 |
0 |
|
\(F\) |
0 |
0 |
0 |
20 |
\(I\) |
0 |
200 |
20 |
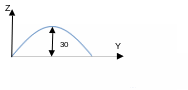
The \(z\) dimension of the plate is defined by the following equation: \(z\mathrm{=}30\mathrm{sin}(2\pi x\mathrm{/}L)\mathrm{sin}(\pi y\mathrm{/}l)\)
1.2. Material properties#
The material has an isotropic elastic behavior:
Young’s module: \(E\mathrm{=}204\mathrm{000.MPa}\)
Poisson’s ratio: \(\nu \mathrm{=}0.3\)
1.3. Boundary conditions and loads#
Boundary conditions:
Embedding on the \(\mathit{GAUCHE}\) side
3D modeling, SHB: 3 cases of surface loads on the \(\mathit{DROITE}\) side:
\(\mathit{fx}\text{}\mathrm{=}\text{}0.5N\mathrm{/}\mathit{mm²}\)
\(\mathit{fy}\text{}\mathrm{=}\text{}0.5N\mathrm{/}\mathit{mm²}\)
\(\mathit{fz}\text{}\mathrm{=}\mathrm{-}0.5N\mathrm{/}\mathit{mm²}\)
Modeling COQUE_3D; 2 cases of linear loads on the \(\mathit{DROITE}\) side
\(\mathit{fx}\text{}\mathrm{=}\text{}10.N\mathrm{/}\mathit{mm}\)
\(\mathit{fz}\text{}\mathrm{=}\mathrm{-}10.N\mathrm{/}\mathit{mm}\)