1. Reference problem#
1.1. Geometry#
3-point flexure
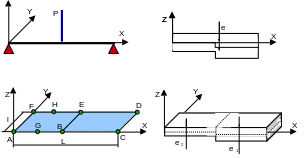
Characteristics of plates \((m)\):
Length: \(L=10\)
Width: \(l=1\)
Thickness 1: \({e}_{1}=0.1\)
Thickness 2: \({e}_{2}=0.08\)
Eccentricity: \(e=0.01\)
Coordinates of points \((m)\):
\(A:(\mathrm{0,0})\) \(E:(\mathrm{5,1})\)
\(B:(\mathrm{5,0})\) \(F:(\mathrm{0,1})\)
\(C:(\mathrm{10,0})\) \(G:(2.5\mathrm{,0})\)
\(D:(\mathrm{10,1})\) \(H:(2.5\mathrm{,1})\)
1.2. Material properties#
Elastic
\(E=2.1\times {10}^{11}\mathrm{Pa}\) Young’s module
\(\nu =0.3\) Poisson’s ratio
1.3. Boundary conditions and loads#
Imposed displacement \((m)\):
segment \(\mathrm{AF},\mathrm{CD}\): \(\mathrm{DZ}=0\)
segment \(\mathrm{FA}\): \(\mathrm{DX}=0\)
point \(A\): \(\mathrm{DX}=\mathrm{DY}=\mathrm{DRZ}=0\)
Loading
Pressure on \(\mathrm{BE}\): \(p=2.\times {10}^{5}N/m\) \(P=\mathrm{pl}\)