1. Reference problem#
1.1. Geometry#
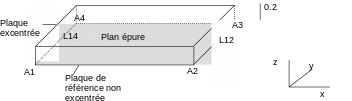
The eccentric plate has been represented here in relation to the draft plane (which here coincides with the lower plane of the eccentric plate).
To avoid overloading the diagram, the non-eccentric reference plate is not drawn, for which the drawing plane is also the mean plane.
1.2. Material properties#
The material constituting plate is characterized by the following data:
\(\mathrm{EL}=\mathrm{20000.Pa}\) |
|
|
\(\nu LN=0.\) \(\nu LT=0\) \(\nu TN=0.\) \(\mathrm{GLT}=\mathrm{2000.Pa}\) \(\mathrm{GLN}=0.\) \(\mathrm{GTN}=0.\)
\(\rho =\mathrm{1000.kg}/{m}^{3}\)
1.3. Boundary conditions and loads#
The \(\mathrm{L14}\) mesh is embedded \(\mathrm{DX}=\mathrm{DY}=\mathrm{DZ}=0.\)
\(\mathrm{DRX}=\mathrm{DRY}=\mathrm{DRZ}=0.\)
We apply the forces to the \(\mathrm{L12}\) mesh
\(\mathrm{FX}=\mathrm{1000.N}\) \(\mathrm{MY}=\mathrm{100.N.m}\) |
on the off-center plate |
\(\mathrm{FX}=\mathrm{1000.N}\) |
on the non-eccentric plate |
These loads are applied using FORCE_ARETE of AFFE_CHAR_MECA in the design plane.
Note:
The fact of applying a force \(\mathrm{FX}\) to the eccentric plate at the level of the design plane generates a moment \(\mathrm{MY}\) that must be compensated in order to end up in purely membrane conditions at the level of the eccentric plate.