1. Reference problem#
1.1. Geometry#
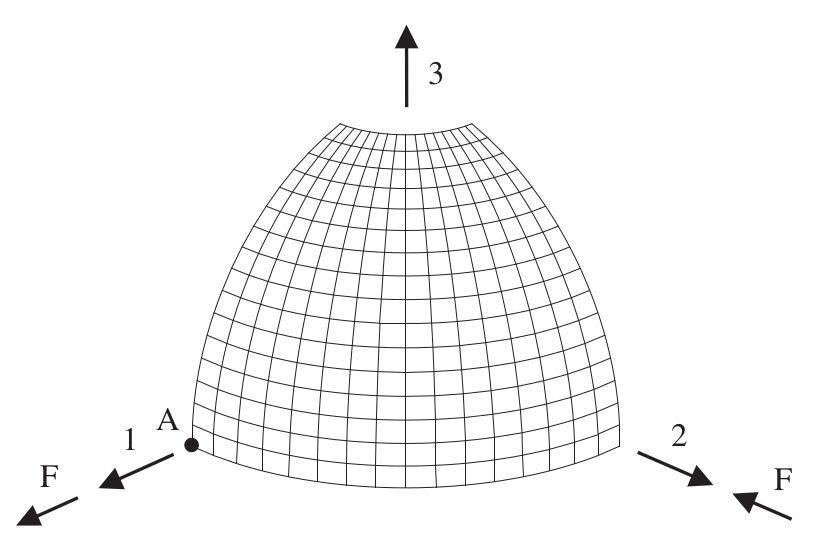
We consider a hemisphere divided into 4 pieces (by symmetry around the equatorial planes).
Radius of the sphere: \(R=10m\)
Thickness of the sphere: \(t=\mathrm{0,04}m\)
The hole is open: 18°
1.2. Material properties#
The sphere is made of aluminum. The material is linear isotropic elastic.
\(E\mathrm{=}6.825{10}^{7}\mathit{Pa}\), \(\nu \mathrm{=}0.3\)
1.3. Boundary conditions and loads#
On a quarter of the hemisphere, symmetry conditions are applied on all three planes (which are therefore QUAD4):
Plan \((12)\): \(\mathit{DZ}=0\);
Plan \((13)\): \(\mathit{DY}=0\);
Plan \((23)\): \(\mathit{DX}=0\).
Moreover, a loading in the form of a point force is applied to points A and B such as:
Point A: \(\mathit{FX}=\mathrm{0,5}N\);
Point B: \(\mathit{FY}=-\mathrm{0,5}N\).