1. Reference problem#
1.1. Geometry#
The geometry, dimensions and materials are taken to be identical to those of Bittencourt et al. [1] and Ventura et al. [2].
Structure \(\mathrm{2D}\) is a rectangular plate (\(20\mathrm{mm}\times 8\mathrm{mm}\)) with 3 holes, including a through crack (). The length of the initial crack is \(a=\mathrm{1,5}\mathrm{mm}\).
The nodes marked \(\mathrm{P1}\), \(\mathrm{P2}\), and \(\mathrm{P3}\) on the serve to impose boundary conditions, which are explained in paragraph [§ 1.3].
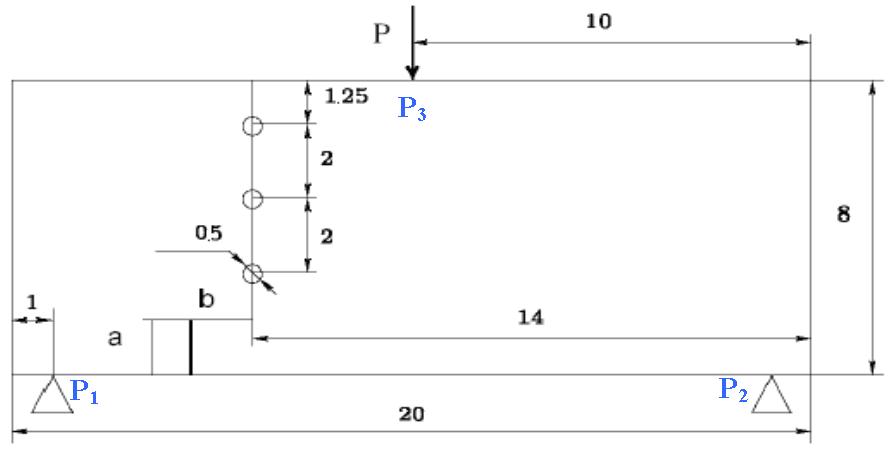
Figure 1.1-1: geometry of the cracked plate
1.2. Material properties#
Young’s module: \(E=205000\mathrm{MPa}\)
Poisson’s ratio: \(\nu \mathrm{=}\mathrm{0,3}\)
1.3. Boundary conditions and loads#
In order to block rigid modes, we block the movements of nodes \(\mathrm{P1}\) and \(\mathrm{P2}\) as follows:
\({\mathrm{DY}}^{\mathrm{P1}}={\mathrm{DY}}^{\mathrm{P2}}=0\);
\({\mathrm{DX}}^{\mathrm{P1}}=0.\)
In order to simulate fatigue propagation, a unit nodal force is applied in \(\mathrm{P3}\): \(\mathit{FY}\mathrm{=}\mathrm{-}1\). A load cycle will correspond to: zero load → max load → zero load. 35 propagation steps are simulated. At each propagation step, the crack advances by an imposed length equal to 0.1 m.
1.4. Benchmark solution#
Given the lack of precision of the diagrams in article [1], it is not possible to derive/to establish precise numerical values. All we have to do is check that the crack paths have the same appearance (see § 2.3).
For the test, the values of the stress intensity factors \({K}_{I}\) and \({K}_{\mathrm{II}}\) calculated by modeling A at the end of propagation are used as a reference:
\(\begin{array}{c}{K}_{I}^{\mathit{ref}}\mathrm{=}\mathrm{1,142045}{\mathit{MPa.mm}}^{\mathrm{0,5}}\\ {K}_{\mathit{II}}^{\mathit{ref}}\mathrm{=}\mathrm{-}\mathrm{0,057097}{\mathit{MPa.mm}}^{\mathrm{0,5}}\end{array}\)
1.5. Bibliographical references#
T.N. Bittencourt, P.A. Wawrzynek, A.R. Ingraffea, A.R. Ingraffea, J.L. Sousa, Quasi-automatic simulation of crack propagation for 2D LEFM problems, Engineering Fracture Mechanics, vol. 55, vol. 55, pp. 321—334, 1996
Ventura, J.X. Xu, T. Belytschko, T. Belytschko, A vector level set method and new discontinuity approximations for crack growth by EFG, International Journal for Numerical Methods in Engineering, vol. 54, vol. 54, pp. 923—944, 2002