2. Modeling A#
In this D_ PLAN modeling, the plate is cracked over half a length. The crack is described by method XFEM. The crack is enriched geometrically, on a radius \({R}_{\mathit{ENRI}}\mathrm{=}\mathrm{0,1}\).
The elements are linear of type TRIA3.
2.1. Characteristics of the mesh#
The unit square is meshed regularly []. To build the mesh, we rely on a regular grid \(100\mathrm{\times }100\).
NOMBRE OF NOEUDS: 10201
NOMBRE OF MAILLES: 20400
TRIA3: 20000

Figure 2.1-1: Meshing with triangle-elements
2.2. Tested sizes and results#
2.2.1. Tested sizes:#
For this horizontal crack, we test the value of the stress intensity factors \({K}_{I}\) and \({K}_{\mathrm{II}}\) as well as the value of the energy restoration rate \(G\) given by CALC_G.
For method \(G-\mathrm{thêta}\) (command CALC_G), the following theta field crown is chosen:
\({R}_{\mathit{inf}}\mathrm{=}\mathrm{0,1}a\) and \({R}_{\text{sup}}\mathrm{=}\mathrm{0,3}a\) where \(a\) is the length of the crack.
On the other hand, we test the displacement field calculated by Code_Aster. Instead of performing a local test on a few cells by TEST_RESU, we test the displacement field on a large number of cells. An arbitrary test area has been delimited in the field [].
In practice, we compare: \({∥{U}^{\mathit{calc}}\mathrm{-}{U}^{\mathit{ana}}∥}_{{L}_{2}}<\mathit{tolerance}\mathrm{\times }{∥{U}^{\mathit{ana}}∥}_{{L}_{2}}\).
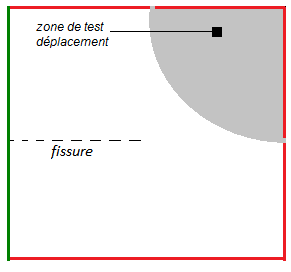
Figure 2.2.1-1: Definition of test GROUP_MA
We are finally testing the energy of the structure, the \({L}^{2}\) travel norm, throughout the field.
2.2.2. Results:#
Stress Intensity Factors Test:
Identification |
Reference |
Tolerance |
CALC_G |
||
K1 |
1.00 |
|
K2 |
0.00 |
|
G |
1.0 10-5 |
|
Testing the standard_L2 of the error on the displacement field: \({\Vert {U}^{\mathit{calc}}-{U}^{\mathit{ana}}\Vert }_{{L}_{2}}<\mathit{tolerance}\times {\Vert {U}^{\mathit{ana}}\Vert }_{{L}_{2}}\)
Identification |
Reference |
Tolerance |
POST_ELEM |
||
NORME |
0.00 |
|
Structure energy test:
Identification |
Reference |
Tolerance |
POST_ERREUR |
||
REFERENCE |
3,50687407712 10-6 |
|
Testing the \({L}^{2}\) travel standard across the field:
Identification |
Reference |
Tolerance |
POST_ERREUR |
||
REFERENCE |
7,6057690825 10-6 |
|
2.3. Additional results:#
On the [], the displacement field is represented with amplification of the movement jump at the interface. We can see that the crack opens rigorously in \(\mathit{mode}I\), as expected.
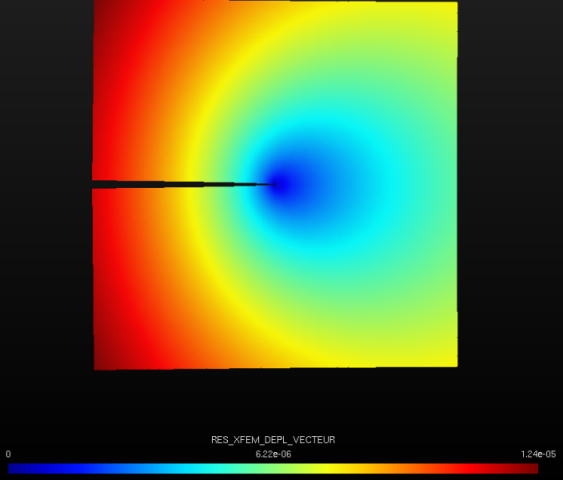
Figure 2.3-1: Field of movement (with offset)