1. Reference problem#

1.1. Geometry#

Geometry of the substructures:

Pavement \(1\)

Pavement \(2\)
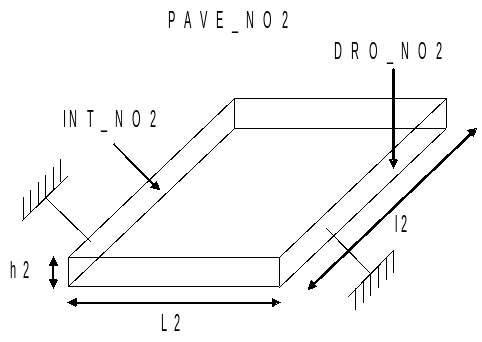
_images/100002000000021B00000128F57F522A6A67B32A.png _images/10000200000001E200000156F70D5E47B4CFB4B6.png

Pavement geometry \((m)\):

\(\mathrm{L1}=1\) \(\mathrm{L2}=0.5\)

\(\mathrm{l1}=0.5\) \(\mathrm{l2}=0.7\)

\(\mathrm{h1}=0.2\) \(\mathrm{h2}=0.2\)

Mesh group:

\(\mathrm{PAVE}\text{\_}\mathrm{NO1}\): set of \(1\) pavement links

\(\mathrm{GOCH}\text{\_}\mathrm{NO1}\): set of meshes forming the left side of the \(1\) block

\(\text{INT}\text{\_}\mathrm{NO1}\): set of cells forming the right side of the \(1\) block

\(\mathrm{PAVE}\text{\_}\mathrm{NO2}\): set of \(2\) pavement links

\(\text{INT}\text{\_}\mathrm{NO2}\): set of meshes forming the left side of the \(2\) block

\(\mathrm{DRO}\text{\_}\mathrm{NO2}\): set of cells forming the right side of the \(2\) block

Structure geometry:

_images/10000200000002C50000010EF432216DDF1C1C6B.png

Mesh group:

\(\text{LINT}\): interface made up of mesh groups \(\text{INT}\text{\_}\mathrm{NO1}\) and \(\text{INT}\text{\_}\mathrm{NO2}\)

1.2. Elastic properties of materials#

      • Block \(1\):

        • \(E=7.1E10\mathrm{Pa}\) Young’s module

        • \(\nu =0.3\) Poisson’s ratio

        • \(\rho =2700.0{\mathrm{kg.m}}^{-3}\) Density

      • Block \(2\):

        • \(E=12.0E10\mathrm{Pa}\) Young’s module

        • \(\nu =0.3\) Poisson’s ratio

        • \(\rho =7820.0{\mathrm{kg.m}}^{-3}\) Density

1.3. Boundary conditions and loads#

    • Imposed displacement in pavement \(1\):

        • \(\mathrm{GOCH}\text{\_}\mathrm{NO1}\) and \(\text{INT}\text{\_}\mathrm{NO1}\): \(\mathrm{DX}=\mathrm{DY}=\mathrm{DZ}=0.0\)

      • Imposed displacement in pavement \(2\):

        • \(\mathrm{DRO}\text{\_}\mathrm{NO2}\) and \(\text{INT}\text{\_}\mathrm{NO2}\): \(\mathrm{DX}=\mathrm{DY}=\mathrm{DZ}=0.0\)

      • Interface pad \(1\):

        • \(\text{INT}\text{\_}\mathrm{NO1}\): \(\mathrm{CRAIGB}\) interface

      • Interface pad \(2\):

        • \(\text{INT}\text{\_}\mathrm{NO2}\): \(\mathrm{CRAIGB}\) interface