1. Reference problem#
1.1. Geometry#
We consider a star with three branches as represented in Figure 1.1-1. The figure also shows the dimensions (in meters) of the structure. The thickness is homogeneous, and is equal to 5 mm.
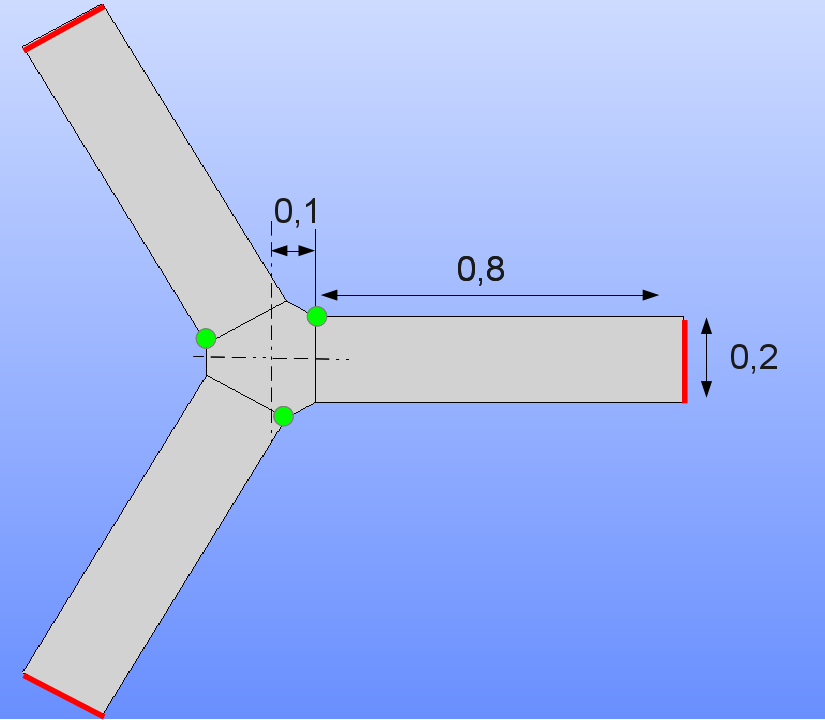
Figure 1.1-1: Star geometry.
1.2. Material properties#
The material constituting each of the substructures is a standard, isotropic elastic steel. Its properties are:
Young’s modulus \(E=210000\mathit{MPa}\)
Poisson’s ratio \(\nu =\mathrm{0,3}\)
density \(\rho =7800\mathit{kg}/{m}^{3}\)
For modeling B, Rayleigh coefficients are introduced to obtain a modal damping of 15% for frequencies located at 10 Hz and 50 Hz, i.e.
\(\{\begin{array}{ccc}\alpha & \text{=}& 2({\xi }_{1}{\omega }_{1}-{\xi }_{2}{\omega }_{2})/({\omega }_{1}^{2}-{\omega }_{2}^{2})\\ \beta & \text{=}& 2{\xi }_{1}{\omega }_{1}-\alpha {\omega }_{1}^{2}\end{array},\) with \(\{\begin{array}{ccccc}{\xi }_{1}=0.15& \text{/}& {f}_{1}=10\mathit{Hz}& \text{/}& {\omega }_{1}=2\pi {f}_{1}\\ {\xi }_{2}=0.15& \text{/}& {f}_{2}=50\mathit{Hz}& \text{/}& {\omega }_{2}=2\pi {f}_{2}\end{array}\mathrm{.}\)
1.3. Boundary conditions and loads#
The structure is embedded on the edges shown in red in figure 1.1-1, and is not loaded (modal calculation without prestress).