1. Reference problem#
1.1. Geometry#
We consider a beam of length \(L=\mathrm{7,62}m\), of rectangular cross section (\(\mathit{Hy}=\mathrm{0,0508}m\) and \(\mathit{Hz}=\mathrm{0,0254}m\)). It is oriented along the \(\mathit{Ox}\) axis.
1.2. Material properties#
The material is isotropic elastic whose properties are:
Young’s modulus: \(E=\mathrm{206,8}{10}^{9}\mathrm{Pa}\)
Poisson’s ratio: \(\nu =\mathrm{0,3}\)
density: \(\rho =\mathrm{7780,0}\mathrm{kg}/{m}^{3}\)
1.3. Boundary conditions and loads#
The beam is embedded at each of its ends.
The load is a seismic excitation perpendicular to the direction of the beam, expressed in the form of an accelerogram. It is taken from a recording of the so-called El Centro earthquake (). The direction of the earthquake is axis \(\mathit{Oy}\). The sample is \(\mathrm{0,01}s\).
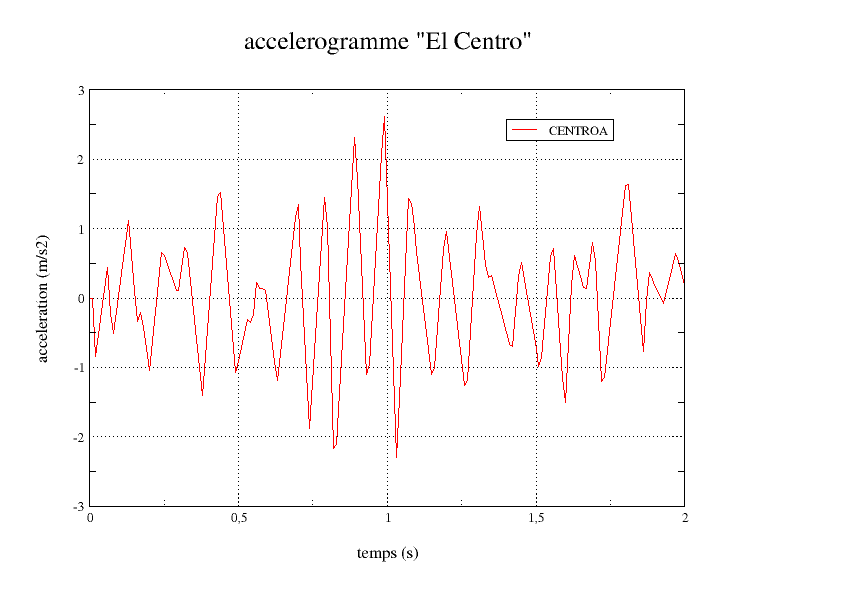
Illustration 1: Accelerogram called « El Centro » taken over 2 s.
For modeling A, single-pressed excitation is considered: the same accelerogram is imposed at both ends of the beam.
For modeling B, a multi-press excitation is considered: the accelerogram imposed at both ends is the same as in mono-press but, in this case, at the opposite end it is applied with a delay of \(\mathrm{0,25}s\) compared to the origin.
1.4. Initial conditions#
The beam is considered to be at rest before the earthquake arrives.