5. D modeling#
5.1. Characteristics of modeling#
This modeling compares the results of Code-Aster spectral modal calculations in multi-support and multi-direction, with or without taking into account the pseudo-mode, with ANSYS results. The different methods of modal accumulation tested are CQC and SRSS. In total, 4 calculations are compared:
calculation 1: SRSS without taking into account the pseudo-mode
calculation 2: CQC without taking into account the pseudo-mode
calculation 3: CQC with pseudo-mode taken into account
calculation 4: SRSS with pseudo-mode taken into account
To be consistent with the model used in ANSYS, the finite element model used in modeling A, B and C is slightly modified at the elbows where the discretization used is finer (Approximately twenty elements per elbow). The other characteristics (thickness, radius, material) are the same as those used in models A, B and C. The flexibility of the pipe is taken into account via the flexibility coefficient by the following formula:
\({c}_{\mathit{flex}}=\frac{\mathrm{1,65}}{\lambda }=\frac{\mathrm{1,65}\ast E\ast {R}_{c}}{{(R-\mathrm{0,5}\ast E)}^{2}}\)
where: \(E\) and \(R\) are the thickness and radius of the pipe cross section and \({R}_{c}\) is the radius of curvature of the elbow.
3D loading is also taken into account in this 3D modeling with the three spectra shown in the following figure:
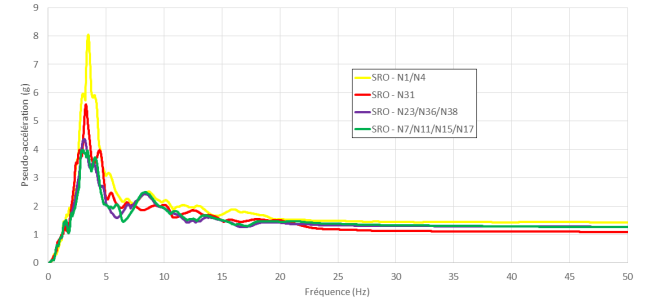
Supports are defined as follows:
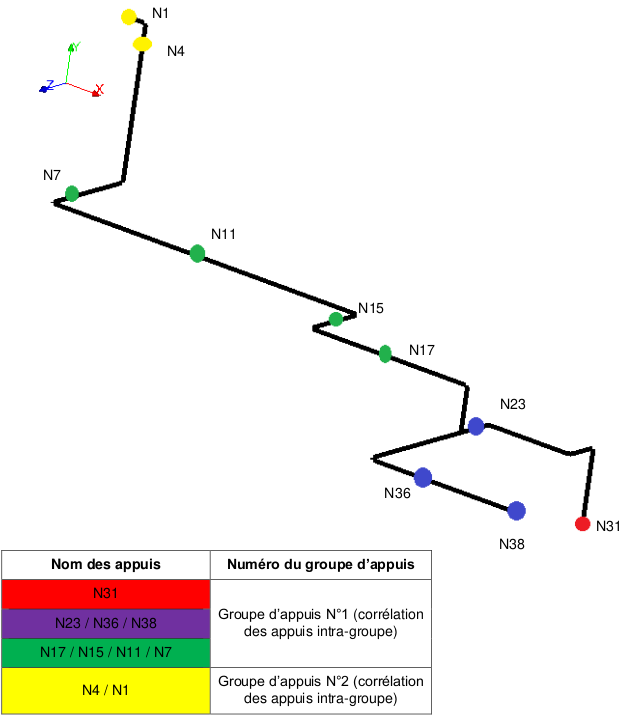
support 1 composed of nodes N1 and N4
support 2 composed of the nodes N7, N11, N15, N17
support 3 composed of the nodes N23, N36, N38
Support 4 composed of the N31 node
The supports are shown in the following figure:
The natural frequencies of the first 25 modes are considered for the calculation of the dynamically amplified part, excluding static correction, for all of the following test cases. Note that the mass matrix remains full (no diagonalization step).
Clean Mode |
Frequencies (Hz) Code-Aster |
1 |
2.9 |
2 |
4.39 |
3 |
4.83 |
4 |
5 |
5 |
6.88 |
6 |
7.44 |
7 |
7.75 |
8 |
10.78 |
9 |
11.41 |
10 |
11.55 |
11 |
12.55 |
12 |
13.9 |
13 |
14.07 |
14 |
14.94 |
1**5** |
16.27 |
1**6** |
17.52 |
1**7** |
20.31 |
1**8** |
21.3 |
1**9** |
21.48 |
2**0** |
22.04 |
2**1** |
22.53 |
2 2 |
23.36 |
2 3 |
23.88 |
2 4 |
27.18 |
2 5 |
29.18 |
5.2. Quantities tested and results by spectral calculation#
5.2.1. Results of calculations without taking into account the pseudo-mode#
The calculations without taking into account the pseudo-mode are carried out by two methods of modal accumulation
calculation 1: SRSS
calculation 2: CQC
The tolerance is calculated by the following formula:
\(\mathit{Tolérance}=\frac{\mathit{Aster}-\mathit{Ansys}}{\mathit{Ansys}}\)
Knots |
Efforts |
Reference calculation 1 (F:lbs, m:lbs-inch) |
Tolerance calculation 1 |
Reference calculation 2 (F:lbs, m:lbs-inch) |
Tolerance calculation 2 |
||
1 |
\(\mathit{FX}\) |
83.1 |
83.1 |
0.02% |
87.6 |
-0.02% |
|
1 |
\(\mathit{FY}\) |
89.3 |
89.3 |
-0.04% |
84.6 |
-0.05% |
|
1 |
\(\mathit{FZ}\) |
141.0 |
141.0 |
0.04 |
0.04% |
60.8 |
-0.02% |
1 |
\(\mathit{MX}\) |
4409.8 |
4409.8 |
0.06% |
1729.9 |
0.00% |
|
1 |
\(\mathit{MY}\) |
3238.6 |
3238.6 |
0.03% |
2184.3 |
-0.02% |
|
1 |
\(\mathit{MZ}\) |
3279.2 |
3279.2 |
-0.01% |
3429.3 |
-0.01% |
|
4 |
\(\mathit{FX}\) |
137.8 |
137.8 |
-0.02% |
141.7 |
-0.03% |
|
4 |
\(\mathit{FZ}\) |
302.7 |
302.7 |
0.04% |
199.1 |
-0.01% |
|
7 |
\(\mathit{FY}\) |
222.7 |
222.7 |
0.02% |
226.7 |
-0.01% |
|
11 |
\(\mathit{FY}\) |
444.3 |
-4.3 |
-0.02% |
469.7 |
-0.01% |
|
11 |
\(\mathit{FZ}\) |
301.5 |
301.5 |
0.04% |
254.3 |
0.00% |
|
15 |
\(\mathit{FX}\) |
1048.5 |
1048.5 |
0.03% |
1169.5 |
-0.02% |
|
17 |
\(\mathit{FY}\) |
207.4 |
207.4 |
-0.03% |
220.4 |
-0.02% |
|
17 |
\(\mathit{FZ}\) |
226.3 |
226.3 |
0.01% |
21.5 |
0.00% |
|
23 |
\(\mathit{FY}\) |
530.8 |
530.8 |
-0.04% |
624.2 |
-0.03% |
|
23 |
\(\mathit{FZ}\) |
660.6 |
660.6 |
-0.03% |
663.1 |
-0.02% |
|
31 |
\(\mathit{FX}\) |
93.4 |
-0.4 |
-0.13% |
92.4 |
-0.07% |
|
31 |
\(\mathit{FY}\) |
172.9 |
172.9 |
-0.04% |
176.0 |
-0.03% |
|
31 |
\(\mathit{FZ}\) |
301.9 |
301.9 |
-0.02% |
296.1 |
-0.02% |
|
31 |
\(\mathit{MX}\) |
23712.1 |
23712.1 |
-0.01% |
23598.1 |
-0.01% |
|
31 |
\(\mathit{MY}\) |
2042.5 |
2042.5 |
0.01% |
2131.2 |
0.04% |
|
31 |
\(\mathit{MZ}\) |
6417.7 |
6417.7 |
-0.05% |
6506.7 |
-0.01% |
|
3 6 |
|
708.7 |
708.7 |
-0.08% |
691.5 |
-0.07% |
|
3 6 |
|
809.5 |
809.5 |
0.02% |
921.9 |
0.02% |
|
3 8 |
|
386.3 |
386.3 |
-0.07% |
495.2 |
-0.05% |
|
3 8 |
|
469.6 |
469.6 |
-0.06% |
474.8 |
-0.07% |
|
3 8 |
|
387.0 |
-0.02% |
-0.02% |
-0.02% |
||
3 8 |
|
10849.9 |
10849.9 |
0.01% |
10648.4 |
0.02% |
|
3 8 |
|
21527.4 |
21527.4 |
-0.01% |
21612.1 |
-0.02% |
|
3 8 |
|
26272.2 |
26272.2 |
-0.05% |
26532.5 |
-0.05% |
5.2.2. Results of the calculations taking into account the pseudo-mode#
The calculations taking into account the pseudo-mode are carried out by two methods of modal accumulation
calculation 3: SRSS
calculation 4: CQC
Knots |
Efforts |
Reference calculation 3 (F:lbs, m:lbs-inch) |
Tolerance calculation 3 |
Calculation reference 4 (F:lbs, m:lbs-inch) |
Tolerance calculation 4 |
|
1 |
\(\mathit{FX}\) |
108.6 |
108.6 |
0.09% |
105.0 |
0.10% |
1 |
\(\mathit{FY}\) |
306.9 |
306.9 |
0.24% |
308.2 |
0.24% |
1 |
\(\mathit{FZ}\) |
87.5 |
87.5 |
0.12% |
154.4 |
0.08% |
1 |
\(\mathit{MX}\) |
1923.3 |
1923.3 |
0.05% |
4489.2 |
0.06% |
1 |
\(\mathit{MY}\) |
2400.5 |
2400.5 |
0.03% |
3388.2 |
0.05% |
1 |
\(\mathit{MZ}\) |
5463.5 |
5463.5 |
5463.5 |
0.16% |
|
4 |
\(\mathit{FX}\) |
177.4 |
17.4 |
0.09% |
174.3 |
0.10% |
4 |
\(\mathit{FZ}\) |
300.4 |
300.4 |
0.14% |
37.1 |
0.11% |
7 |
\(\mathit{FY}\) |
239.0 |
0.03% |
235.3 |
0.02% |
|
11 |
\(\mathit{FY}\) |
482.9 |
482.9 |
0.01% |
458.2 |
0.00% |
11 |
\(\mathit{FZ}\) |
260.8 |
260.8 |
0.01% |
307.0 |
0.05% |
15 |
\(\mathit{FX}\) |
1170.6 |
1170.6 |
0.02% |
1049.6 |
-0.03% |
17 |
\(\mathit{FY}\) |
228.5 |
228.5 |
0.01% |
216.1 |
0.01% |
17 |
\(\mathit{FZ}\) |
240.4 |
240.4 |
0.07% |
253.5 |
0.08% |
23 |
\(\mathit{FY}\) |
686.6 |
686.6 |
0.02% |
603.0 |
0.03% |
23 |
\(\mathit{FZ}\) |
667.4 |
-0.01% |
-0.01% |
664.9 |
-0.03% |
31 |
\(\mathit{FX}\) |
110.7 |
110.7 |
0.01% |
111.5 |
-0.04% |
31 |
\(\mathit{FY}\) |
240.5 |
240.5 |
0.05% |
238.2 |
0.05% |
31 |
\(\mathit{FZ}\) |
299.8 |
299.8 |
-0.02% |
305.5 |
-0.02% |
31 |
\(\mathit{MX}\) |
23614.7 |
23614.7 |
-0.01% |
23728.7 |
-0.01% |
31 |
\(\mathit{MY}\) |
2132.8 |
2132.8 |
0.04% |
2044.1 |
0.01% |
31 |
\(\mathit{MZ}\) |
6584.2 |
6584.2 |
0.00% |
6496.3 |
-0.04% |
3 6 |
|
792.3 |
792.3 |
0.06% |
807.4 |
0.05% |
3 6 |
|
922.0 |
0.02% |
809.6 |
0.02% |
|
3 8 |
|
1501.0 |
1501.0 |
0.20% |
1468.7 |
0.21% |
3 8 |
|
531.6 |
531.6 |
0.01% |
527.0 |
0.02% |
3 8 |
|
415.5 |
415.5 |
0.02% |
420.6 |
0.02% |
3 8 |
|
10660.1 |
10660.1 |
0.02% |
10861.4 |
0.01% |
3 8 |
|
21803.5 |
21803.5 |
-0.01% |
-0.01% |
|
3 8 |
|
26872.7 |
26872.7 |
-0.04% |
26615.7 |
-0.04% |