1. Reference problem

1.1. Geometry

A rotor model supported by 2 bearings (nodes \(\mathrm{B1}\) and \(\mathrm{B2}\) in the figure below), whose stiffness and damping matrices are non-symmetric. It is composed of 3 disks, and 4 shaft sections.

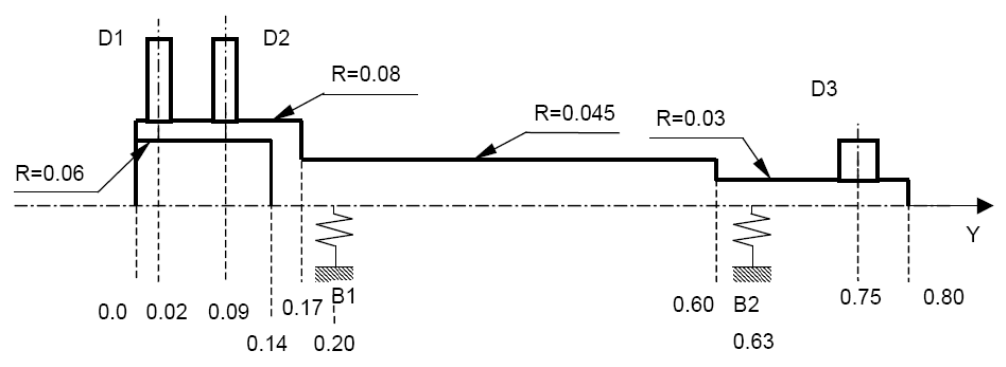
Figure 1.1-a -a: Rotor model with 3 disks and 2 asymmetric bearings

1.2. Material properties

The geometric and material characteristics are listed in the following table.

Material		\(E={2.10}^{11}N/{m}^{2}\)	\(\rho =7800\mathrm{kg}/{m}^{3}\)	\(\nu =0.3\)
Disc	\(\mathrm{D1}\)	\(M=20\mathrm{kg}\)	\({I}_{D}=200.{10}^{-3}\mathrm{kg}{m}^{2}\)	\({I}_{P}={400.10}^{-3}\mathrm{kg}{m}^{2}\)
	\(\mathrm{D2}\)	\(M=17\mathrm{kg}\)	\({I}_{D}=170.{10}^{-3}\mathrm{kg}{m}^{2}\)	\({I}_{P}={340.10}^{-3}\mathrm{kg}{m}^{2}\)
	\(\mathrm{D3}\)	\(M=10\mathrm{kg}\)	\({I}_{D}=15.{10}^{-3}\mathrm{kg}{m}^{2}\)	\({I}_{P}=30.{10}^{-3}\mathrm{kg}{m}^{2}\)

The characteristics of the levels are given in the tables that follow.

\(\Omega =0\mathrm{tr}/\mathrm{min}\)

Level	\(\mathrm{P1}\)	\({K}_{\mathrm{yy}}={90.10}^{6}N/m\)	\({K}_{\mathit{xx}}\mathrm{=}{50.10}^{7}N\mathrm{/}m\)
		\({K}_{\mathit{yx}}\mathrm{=}\mathrm{-}{8.10}^{4}N\mathrm{/}m\)	\({K}_{\mathit{xy}}\mathrm{=}{9.10}^{4}N\mathrm{/}m\)
		\({c}_{\mathrm{yy}}=15.{10}^{4}\mathrm{Ns}/m\)	\({c}_{\mathit{xx}}\mathrm{=}45.{10}^{4}\mathit{Ns}\mathrm{/}m\)
		\({c}_{\mathit{yx}}\mathrm{=}1.{10}^{2}\mathit{Ns}\mathrm{/}m\)	\({c}_{\mathit{xy}}\mathrm{=}\mathrm{-}{1.10}^{2}\mathit{Ns}\mathrm{/}m\)
Level	\(\mathrm{P2}\)	\({K}_{\mathrm{yy}}={60.10}^{6}N/m\)	\({K}_{\mathit{xx}}\mathrm{=}{15.10}^{7}N\mathrm{/}m\)
		\({K}_{\mathit{yx}}\mathrm{=}\mathrm{-}{8.10}^{4}N\mathrm{/}m\)	\({K}_{\mathit{xy}}\mathrm{=}{8.10}^{4}N\mathrm{/}m\)
		\({c}_{\mathrm{yy}}=12.{10}^{4}\mathrm{Ns}/m\)	\({c}_{\mathit{xx}}\mathrm{=}19.{10}^{4}\mathit{Ns}\mathrm{/}m\)
		\({c}_{\mathit{yx}}\mathrm{=}1.{10}^{2}\mathit{Ns}\mathrm{/}m\)	\({c}_{\mathit{xy}}\mathrm{=}\mathrm{-}{1.10}^{2}\mathit{Ns}\mathrm{/}m\)

\(\Omega =5000\mathrm{tr}/\mathrm{min}\)

Level	\(\mathrm{P1}\)	\({K}_{\mathrm{yy}}={90.10}^{6}N/m\)	\({K}_{\mathit{xx}}\mathrm{=}{50.10}^{7}N\mathrm{/}m\)
		\({K}_{\mathit{yx}}\mathrm{=}\mathrm{-}{9.10}^{4}N\mathrm{/}m\)	\({K}_{\mathit{xy}}\mathrm{=}{9.10}^{4}N\mathrm{/}m\)
		\({c}_{\mathrm{yy}}=15.{10}^{4}\mathrm{Ns}/m\)	\({c}_{\mathit{xx}}\mathrm{=}45.{10}^{4}\mathit{Ns}\mathrm{/}m\)
		\({c}_{\mathit{yx}}\mathrm{=}1.{10}^{2}\mathit{Ns}\mathrm{/}m\)	\({c}_{\mathit{xy}}\mathrm{=}\mathrm{-}{1.10}^{2}\mathit{Ns}\mathrm{/}m\)
Level	\(\mathrm{P2}\)	\({K}_{\mathrm{yy}}={60.10}^{6}N/m\)	\({K}_{\mathit{xx}}\mathrm{=}{15.10}^{7}N\mathrm{/}m\)
		\({K}_{\mathit{yx}}\mathrm{=}\mathrm{-}{8.10}^{4}N\mathrm{/}m\)	\({K}_{\mathit{xy}}\mathrm{=}{8.10}^{4}N\mathrm{/}m\)
		\({c}_{\mathrm{yy}}=12.{10}^{4}\mathrm{Ns}/m\)	\({c}_{\mathit{xx}}\mathrm{=}19.{10}^{4}\mathit{Ns}\mathrm{/}m\)
		\({c}_{\mathit{yx}}\mathrm{=}1.{10}^{2}\mathit{Ns}\mathrm{/}m\)	\({c}_{\mathit{xy}}\mathrm{=}\mathrm{-}{1.10}^{2}\mathit{Ns}\mathrm{/}m\)

\(\Omega =6500\mathrm{tr}/\mathrm{min}\)

Level	\(\mathrm{P1}\)	\({K}_{\mathrm{yy}}={100.10}^{6}N/m\)	\({K}_{\mathit{xx}}\mathrm{=}{40.10}^{7}N\mathrm{/}m\)
		\({K}_{\mathit{yx}}\mathrm{=}\mathrm{-}{15.10}^{4}N\mathrm{/}m\)	\({K}_{\mathit{xy}}\mathrm{=}{15.10}^{4}N\mathrm{/}m\)
		\({c}_{\mathrm{yy}}=13.{10}^{4}\mathrm{Ns}/m\)	\({c}_{\mathit{xx}}\mathrm{=}33.{10}^{4}\mathit{Ns}\mathrm{/}m\)
		\({c}_{\mathit{yx}}\mathrm{=}1.{10}^{2}\mathit{Ns}\mathrm{/}m\)	\({c}_{\mathit{xy}}\mathrm{=}\mathrm{-}{1.10}^{2}\mathit{Ns}\mathrm{/}m\)
Level	\(\mathrm{P2}\)	\({K}_{\mathrm{yy}}={70.10}^{6}N/m\)	\({K}_{\mathit{xx}}\mathrm{=}{14.10}^{7}N\mathrm{/}m\)
		\({K}_{\mathit{yx}}\mathrm{=}\mathrm{-}{13.10}^{4}N\mathrm{/}m\)	\({K}_{\mathit{xy}}\mathrm{=}{13.10}^{4}N\mathrm{/}m\)
		\({c}_{\mathrm{yy}}=10.{10}^{4}\mathrm{Ns}/m\)	\({c}_{\mathit{xx}}\mathrm{=}15.{10}^{4}\mathit{Ns}\mathrm{/}m\)
		\({c}_{\mathit{yx}}\mathrm{=}1.{10}^{2}\mathit{Ns}\mathrm{/}m\)	\({c}_{\mathit{xy}}\mathrm{=}\mathrm{-}{1.10}^{2}\mathit{Ns}\mathrm{/}m\)

\(\Omega =8000\mathrm{tr}/\mathrm{min}\)

Level	\(\mathrm{P1}\)	\({K}_{\mathrm{yy}}={110.10}^{6}N/m\)	\({K}_{\mathit{xx}}\mathrm{=}{35.10}^{7}N\mathrm{/}m\)
		\({K}_{\mathit{yx}}\mathrm{=}\mathrm{-}{20.10}^{4}N\mathrm{/}m\)	\({K}_{\mathit{xy}}\mathrm{=}{20.10}^{4}N\mathrm{/}m\)
		\({c}_{\mathrm{yy}}=11.{10}^{4}\mathrm{Ns}/m\)	\({c}_{\mathit{xx}}\mathrm{=}26.{10}^{4}\mathit{Ns}\mathrm{/}m\)
		\({c}_{\mathit{yx}}\mathrm{=}2.{10}^{2}\mathit{Ns}\mathrm{/}m\)	\({c}_{\mathit{xy}}\mathrm{=}\mathrm{-}{2.10}^{2}\mathit{Ns}\mathrm{/}m\)
Level	\(\mathrm{P2}\)	\({K}_{\mathrm{yy}}={80.10}^{6}N/m\)	\({K}_{\mathit{xx}}\mathrm{=}{14.10}^{7}N\mathrm{/}m\)
		\({K}_{\mathit{yx}}\mathrm{=}\mathrm{-}{20.10}^{4}N\mathrm{/}m\)	\({K}_{\mathit{xy}}\mathrm{=}{20.10}^{4}N\mathrm{/}m\)
		\({c}_{\mathrm{yy}}=9.{10}^{4}\mathrm{Ns}/m\)	\({c}_{\mathit{xx}}\mathrm{=}13.{10}^{4}\mathit{Ns}\mathrm{/}m\)
		\({c}_{\mathit{yx}}\mathrm{=}2.{10}^{2}\mathit{Ns}\mathrm{/}m\)	\({c}_{\mathit{xy}}\mathrm{=}\mathrm{-}{2.10}^{2}\mathit{Ns}\mathrm{/}m\)

\(\Omega =10000\mathrm{tr}/\mathrm{min}\)

Level	\(\mathrm{P1}\)	\({K}_{\mathrm{yy}}={115.10}^{6}N/m\)	\({K}_{\mathit{xx}}\mathrm{=}{33.10}^{7}N\mathrm{/}m\)
		\({K}_{\mathit{yx}}\mathrm{=}\mathrm{-}{35.10}^{4}N\mathrm{/}m\)	\({K}_{\mathit{xy}}\mathrm{=}{35.10}^{4}N\mathrm{/}m\)
		\({c}_{\mathrm{yy}}=10.{10}^{4}\mathrm{Ns}/m\)	\({c}_{\mathit{xx}}\mathrm{=}20.{10}^{4}\mathit{Ns}\mathrm{/}m\)
		\({c}_{\mathit{yx}}\mathrm{=}2.{10}^{2}\mathit{Ns}\mathrm{/}m\)	\({c}_{\mathit{xy}}\mathrm{=}\mathrm{-}{3.10}^{2}\mathit{Ns}\mathrm{/}m\)
Level	\(\mathrm{P2}\)	\({K}_{\mathrm{yy}}={90.10}^{6}N/m\)	\({K}_{\mathit{xx}}\mathrm{=}{14.10}^{7}N\mathrm{/}m\)
		\({K}_{\mathit{yx}}\mathrm{=}\mathrm{-}{30.10}^{4}N\mathrm{/}m\)	\({K}_{\mathit{xy}}\mathrm{=}{30.10}^{4}N\mathrm{/}m\)
		\({c}_{\mathrm{yy}}=8.{10}^{4}\mathrm{Ns}/m\)	\({c}_{\mathit{xx}}\mathrm{=}10.{10}^{4}\mathit{Ns}\mathrm{/}m\)
		\({c}_{\mathit{yx}}\mathrm{=}2.{10}^{2}\mathit{Ns}\mathrm{/}m\)	\({c}_{\mathit{xy}}\mathrm{=}\mathrm{-}{2.10}^{2}\mathit{Ns}\mathrm{/}m\)

\(\Omega =14000\mathrm{tr}/\mathrm{min}\)

Level	\(\mathrm{P1}\)	\({K}_{\mathrm{yy}}={120.10}^{6}N/m\)	\({K}_{\mathit{xx}}\mathrm{=}{30.10}^{7}N\mathrm{/}m\)
		\({K}_{\mathit{yx}}\mathrm{=}\mathrm{-}{70.10}^{4}N\mathrm{/}m\)	\({K}_{\mathit{xy}}\mathrm{=}{70.10}^{4}N\mathrm{/}m\)
		\({c}_{\mathrm{yy}}=7.{10}^{4}\mathrm{Ns}/m\)	\({c}_{\mathit{xx}}\mathrm{=}15.{10}^{4}\mathit{Ns}\mathrm{/}m\)
		\({c}_{\mathit{yx}}\mathrm{=}3.{10}^{2}\mathit{Ns}\mathrm{/}m\)	\({c}_{\mathit{xy}}\mathrm{=}\mathrm{-}{4.10}^{2}\mathit{Ns}\mathrm{/}m\)
Level	\(\mathrm{P2}\)	\({K}_{\mathrm{yy}}={100.10}^{6}N/m\)	\({K}_{\mathit{xx}}\mathrm{=}{14.10}^{7}N\mathrm{/}m\)
		\({K}_{\mathit{yx}}\mathrm{=}\mathrm{-}{60.10}^{4}N\mathrm{/}m\)	\({K}_{\mathit{xy}}\mathrm{=}{60.10}^{4}N\mathrm{/}m\)
		\({c}_{\mathrm{yy}}=6.{10}^{4}\mathrm{Ns}/m\)	\({c}_{\mathit{xx}}\mathrm{=}8.{10}^{4}\mathit{Ns}\mathrm{/}m\)
		\({c}_{\mathit{yx}}\mathrm{=}3.{10}^{2}\mathit{Ns}\mathrm{/}m\)	\({c}_{\mathit{xy}}\mathrm{=}\mathrm{-}{3.10}^{2}\mathit{Ns}\mathrm{/}m\)

1.3. Boundary conditions

To block rigid body movements in the \(z\) direction, we block the degrees of freedom \(\mathit{DZ}\) and \(\mathit{DRZ}\) at the level node \(\mathrm{B1}\).