3. Modeling A#
3.1. Characteristics of modeling#
It is a rotating shaft system with positive rotation speeds.
3.2. Characteristics of the mesh#
The rotor is meshed in 21 finite shaft elements of type POU_D_T and includes 5 discrete elements of type DIS_TR for modeling disks and bearings.
Number of knots: 22
Number and type of elements: 21 SEG2
5 POI1
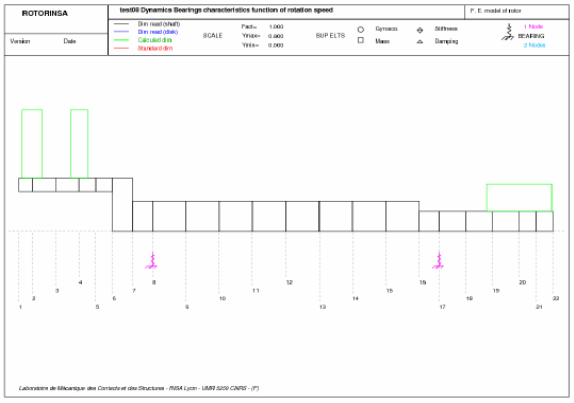
Figure 1-b: Characteristic of the finite element model under ROTORINSA
3.3. Tested sizes and results#
Natural frequencies as a function of rotation speed (direct calculation) :
The values of the first 8 bending frequencies for speeds \(0\mathrm{tr}/\mathrm{mn}\) and \(20000\mathrm{tr}/\mathrm{mn}\), for both software programs, are shown in the table below.
Freq number in flexion |
Rotation speed ( \(\mathrm{tr}/\mathrm{min}\) ) |
ROTORINSA |
Aster_code |
||
\(F(\mathrm{Hz})\) |
Depreciation factor |
\(F(\mathrm{Hz})\) |
Depreciation reduced |
||
1 |
0 |
130.695 |
6.37866E-01 |
131.547 |
6.37613E-01 |
20000 |
123.683 |
1.24817E-01 |
123.706 |
1.24678E-01 |
|
2 |
0 |
227.925 |
9.58757E-02 |
227.716 |
9.49991E-02 |
20000 |
200.581 |
2.17961E-01 |
200.728 |
2.17632E-01 |
|
3 |
0 |
313.311 |
2.27364E-01 |
313.935 |
2.27701E-01 |
20000 |
286.743 |
1.81652E-01 |
286.912 |
1.81388E-01 |
|
4 |
0 |
381.529 |
6.52812E-01 |
375.305 |
6.61825E-01 |
20000 |
308.624 |
4.32727E-01 |
309.825 |
4.31714E-01 |
|
5 |
0 |
390.802 |
1.77361E-01 |
390.241 |
1.74485E-01 |
20000 |
370.338 |
2.54912E-01 |
369.917 |
2.54178E-01 |
|
6 |
0 |
1448.01 |
1.42312E-01 |
1439.66 |
1.54371E-01 |
20000 |
409.861 |
5.58764E-01 |
412.422 |
5.63110E-01 |
|
7 |
0 |
1554.84 |
1.07354E-01 |
1554.35 |
1.11688E-01 |
20000 |
813.124 |
4.73230E-01 |
824.952 |
4.70031E-01 |
|
8 |
0 |
2050.12 |
3.08294E-01 |
1928.78 |
3.04586E-01 |
20000 |
997.312 |
4.93828E-01 |
1006.17 |
5.08301E-01 |
|
The relative tolerance criteria are 10% on the results when stopped and 5% on the results at 20000 rpm. With the exception of tolerance, the frequencies obtained are in line with those of ROTORINSA.
Natural frequencies as a function of the speed of rotation (calculation in 2 stages) :
The values of the first 8 bending frequencies for speeds \(0\mathrm{tr}/\mathrm{mn}\) and \(20000\mathrm{tr}/\mathrm{mn}\), for both software programs, are shown in the table below.
Freq number in flexion |
Rotation speed ( \(\mathrm{tr}/\mathrm{min}\) ) |
ROTORINSA |
Aster_code |
||
\(F(\mathrm{Hz})\) |
Depreciation factor |
\(F(\mathrm{Hz})\) |
Depreciation reduced |
||
1 |
0 |
130.695 |
6.37866E-01 |
130.909 |
6.37982E-01 |
20000 |
123.683 |
1.24817E-01 |
123.701 |
1.24816E-01 |
|
2 |
0 |
227.925 |
9.58757E-02 |
227.890 |
9.56146E-02 |
20000 |
200.581 |
2.17961E-01 |
200.634 |
2.17876E-01 |
|
3 |
0 |
313.311 |
2.27364E-01 |
313.433 |
2.27817E-01 |
20000 |
286.743 |
1.81652E-01 |
286.805 |
1.81739E-01 |
|
4 |
0 |
381.529 |
6.52812E-01 |
380.699 |
6.55069E-01 |
20000 |
308.624 |
4.32727E-01 |
308.825 |
4.32616E-01 |
|
5 |
0 |
390.802 |
1.77361E-01 |
390.883 |
1.76940E-01 |
20000 |
370.338 |
2.54912E-01 |
370.399 |
2.54825E-01 |
|
6 |
0 |
1448.01 |
1.42312E-01 |
1448.54 |
1.45247E-01 |
20000 |
409.861 |
5.58764E-01 |
410.199 |
5.60285E-01 |
|
7 |
0 |
1554.84 |
1.07354E-01 |
1556.64 |
1.07779E-01 |
20000 |
813.124 |
4.73230E-01 |
814.475 |
4.72976E-01 |
|
8 |
0 |
2050.12 |
3.08294E-01 |
2009.06 |
3.09277E-01 |
20000 |
997.312 |
4.93828E-01 |
998.343 |
4.95564E-01 |
|
Table 2-b: Flexion-type natural frequencies for ROTORINSA and Code_Aster (calculation in 2 stages)
The relative tolerance criteria are 5% on the results when stopped and 1% on the results at 20000 rpm. With the exception of tolerance, the frequencies obtained are in better agreement with those of ROTORINSA (compared to the direct modal calculation method). Indeed, it is this method of modal calculation in 2 floors that is used in ROTORINSA.
In Code_Aster, we also observe frequencies and modes of twisting and modes of traction/compression. These modes are not calculated by ROTORINSA, as it only models bending behavior.
The values of the first torsional frequency for speeds \(0\mathrm{tr}/\mathrm{mn}\) and \(20000\mathrm{tr}/\mathrm{mn}\), for Code_Aster, are shown in the table below
Torsion Freq Number |
Rotation speed (rpm) |
\(F(\mathrm{Hz})\) |
1 |
0 |
5.81803E+02 |
20000 |
5.81803E+02 |
Table 2-c: Torsion frequencies given by Code_Aster
The value of the first traction frequency for speeds \(0\mathrm{tr}/\mathrm{mn}\) and \(20000\mathrm{tr}/\mathrm{mn}\), for Code_Aster, are shown in the table below
Torsion Freq Number |
Rotation speed (rpm) |
\(F(\mathrm{Hz})\) |
1 |
0 |
1.67224E+03 |
20000 |
1.67224E+03 |
Table 2-c: Traction frequencies given by Code_Aster
In summary, in the table below, the numbers and frequencies calculated and used in the plot of the Campbell diagram in Code_Aster are presented.
Number of eigenvalues detected: 12
Number of frequencies requested for the route: 8
calculated |
plotted |
|
Number of total frequencies |
12 |
8 |
Number of frequencies in bending |
8 |
7 |
Torsion frequency number |
1 |
1 |
Number of traction/compression frequencies |
1 |
0 |
Table 2-d: Frequencies calculated and plotted (Code_Aster)