1. Reference problem#
1.1. Geometry#
A rotor model supported by 2 bearings (nodes \(\mathrm{B1}\) and \(\mathrm{B2}\) in the figure below), whose stiffness and damping matrices are non-symmetric. It is composed of 3 discs and 4 shaft sections.
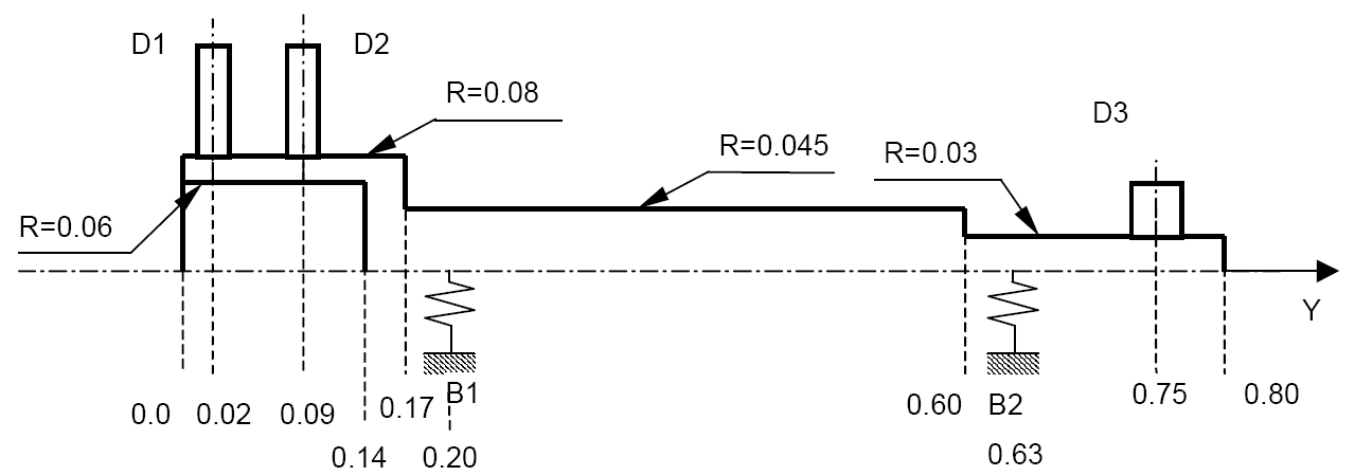
1.2. Material properties#
The geometric and material characteristics are listed in the following table.
Material |
\(E=2{10}^{11}N/{m}^{2}\) |
\(\rho =7800\mathrm{kg}/{m}^{3}\) |
\(\nu =0.3\) |
|
Disc |
\(\mathrm{D1}\) |
\(M=20\mathrm{kg}\) |
\({I}_{D}=\mathrm{0,20}\mathrm{kg}{m}^{2}\) |
\({I}_{P}=\mathrm{0,40}\mathrm{kg}{m}^{2}\) |
\(\mathrm{D2}\) |
\(M=17\mathrm{kg}\) |
\({I}_{D}=\mathrm{0,17}\mathrm{kg}{m}^{2}\) |
\({I}_{P}=\mathrm{0,34}\mathrm{kg}{m}^{2}\) |
|
\(\mathrm{D3}\) |
\(M=10\mathrm{kg}\) |
\({I}_{D}=\mathrm{0,015}\mathrm{kg}{m}^{2}\) |
\({I}_{P}=\mathrm{0,30}\mathrm{kg}{m}^{2}\) |
|
The characteristics of the bearings vary linearly according to the speed of rotation:
to \(5000\mathrm{tr}/\mathrm{min}\):
Level |
\(\mathrm{P1}\) |
|
|
\(\mathrm{kyz}=9{10}^{4}N/m\) |
|
||
\(\mathrm{cyy}=\mathrm{1,5}{10}^{5}\mathrm{Ns}/m\) |
|
||
\(\mathrm{cyz}=-1{10}^{2}\mathrm{Ns}/m\) |
|
||
Level |
\(\mathrm{P2}\) |
|
|
\(\mathrm{kyz}=8{10}^{4}N/m\) |
|
||
\(\mathrm{cyy}=\mathrm{1,2}{10}^{5}\mathrm{Ns}/m\) |
|
||
\(\mathrm{cyz}=-1{10}^{2}\mathrm{Ns}/m\) |
|
to \(6500\mathrm{tr}/\mathrm{min}\):
Level |
\(\mathrm{P1}\) |
|
|
\(\mathrm{kyz}=\mathrm{1,5}{10}^{5}N/m\) |
|
||
\(\mathrm{cyy}=\mathrm{1,3}{10}^{5}\mathrm{Ns}/m\) |
|
||
\(\mathrm{cyz}=-1{10}^{2}\mathrm{Ns}/m\) |
|
||
Level |
P2 |
|
|
\(\mathrm{kyz}=\mathrm{1,3}{10}^{5}N/m\) |
|
||
\(\mathrm{cyy}=1{10}^{5}\mathrm{Ns}/m\) |
|
||
\(\mathrm{cyz}=-1{10}^{2}\mathrm{Ns}/m\) |
|
1.3. Boundary conditions#
To block rigid body movements in direction \(x\), we block the degree of freedom \(\mathrm{DX}\) at the level node \(\mathrm{B1}\).