1. Reference problem#

1.1. Geometry#

The chimney is a vertical beam of length \(10m\), embedded at its base and articulated at two altitude points \(4m\) and \(8m\).

_images/Object_1.svg

Beam cross section:

Area: \(A\mathrm{=}3.4390{10}^{\mathrm{-}3}{m}^{2}\)

Moments of inertia: \({I}_{y}\mathrm{=}\mathrm{1.3770.}{10}^{\mathrm{-}5}{m}^{4}\)

\({I}_{z}\mathrm{=}\mathrm{1.3770.}{10}^{\mathrm{-}5}{m}^{4}\)

\({J}_{x}\mathrm{=}2.7540{10}^{\mathrm{-}5}{m}^{4}\)

1.2. Material properties#

Beam

Young’s module density Poisson’s ratio

\(E\mathrm{=}1.658{10}^{11}\mathit{Pa}\) \(\rho \mathrm{=}1.3404106{10}^{4}\mathit{kg}\mathrm{/}{m}^{3}\) \(\nu \mathrm{=}\mathrm{0,3}\)

1.3. Boundary conditions and loads#

Modeling A (3D)

Embedded point \(\mathit{N1}\): \(\mathit{DX}\mathrm{=}\mathit{DY}\mathrm{=}\mathit{DZ}\mathrm{=}\mathit{DRX}\mathrm{=}\mathit{DRY}\mathrm{=}\mathit{DRZ}\mathrm{=}0\)

Points \(\mathit{N5}\) and \(\mathit{N9}\) attached: \(\mathit{DX}\mathrm{=}\mathit{DY}\mathrm{=}0\)

Spectra of horizontal oscillators under acceleration applied to points \(\mathit{N1}\), \(\mathit{N5}\) and \(\mathit{N9}\) in the (\(x\)) and (\(x\) and \(y\)) directions.

Modeling B (2D plane \(\mathit{XZ}\))

Problem plan \(\mathit{XZ}\): \(\mathit{DY}\mathrm{=}\mathit{DRX}\mathrm{=}\mathit{DRZ}\mathrm{=}0\)

Embedded point \(\mathit{N1}\): \(\mathit{DX}\mathrm{=}\mathit{DZ}\mathrm{=}\mathit{DRY}\mathrm{=}0\)

Points \(\mathit{N5}\) and \(\mathit{N9}\) attached: \(\mathit{DX}\mathrm{=}0\)

Spectra of accelerating horizontal oscillators applied to points \(\mathit{N1}\), \(\mathit{N5}\) and \(\mathit{N9}\) in the (\(x\)) direction.

Spectra of identical values for the 3 amortizations \(\text{0,5\%}\), \(\text{1\%}\) and \(\text{1,5\%}\).

Frequency (\(\mathit{Hz}\))

Pseudo-acceleration (\({\mathit{m.s}}^{\mathrm{-}2}\)) in \(x\)

Pseudo-acceleration (\({\mathit{m.s}}^{\mathrm{-}2}\)) in \(y\)

1 10 30 100 10000

1.962 19.62 19.62 1.962 1.962

1.962 19.62 19.62 1.962 1.962
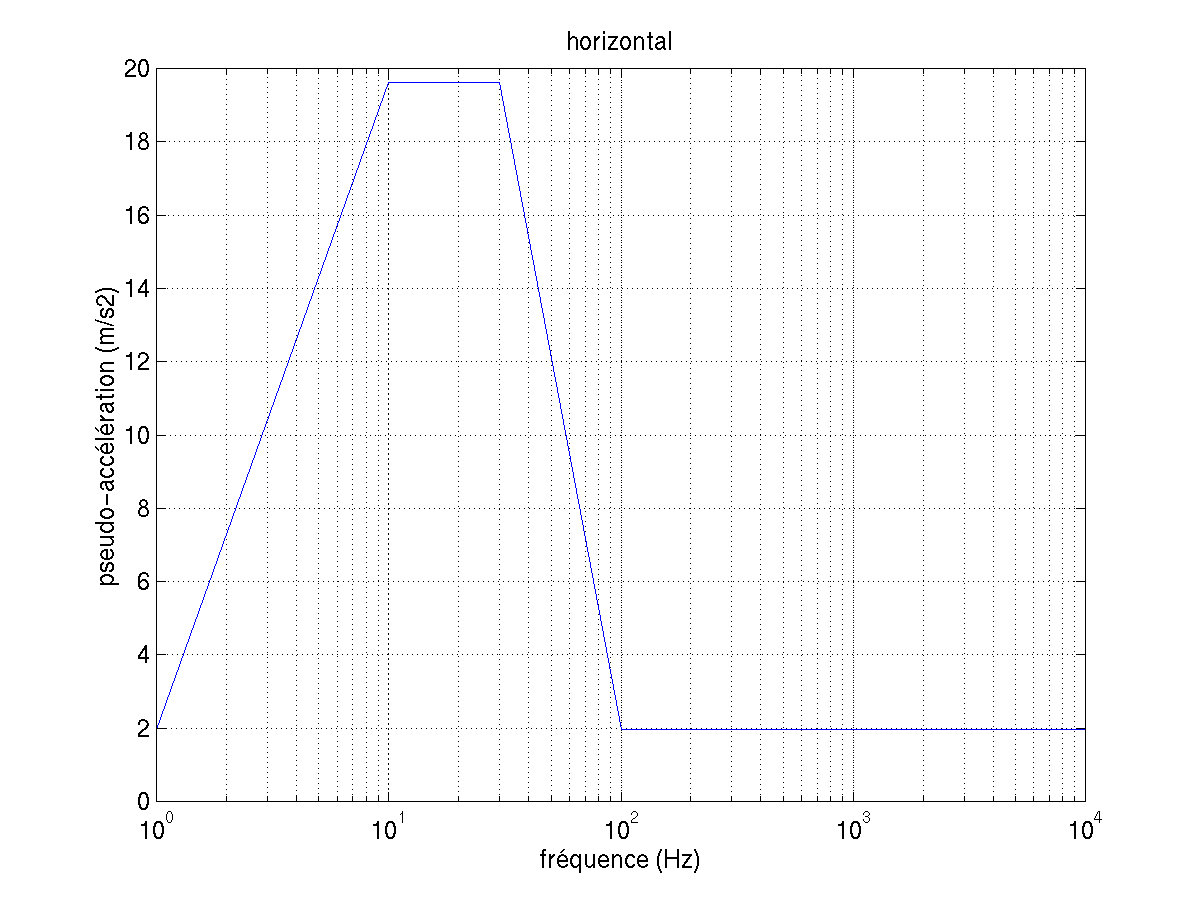
_images/10000000000004B0000003859F35062EEE4E3B0F.png

For the calculation, a damping reduced by 3% is used, with an interpolation (LOG LOG) in frequency and (LIN LOG) in damping.

Multi-support case with different excitations:

point \(\mathit{N1}\): excitement \(1\)

point \(\mathit{N5}\): excitement \(\mathrm{\times }1.5\)

point \(\mathit{N9}\): excitement \(\mathrm{\times }2\)

1.4. Initial conditions#

Not applicable for spectral analysis