1. Reference problem#

1.1. Geometry#

_images/Shape1.gif

Geometry of the \((m)\) beam:

\(L=1.5\)

\(R=0.005\)

\({e}_{p}=0.0005\)

Coordinates of points \((m)\):

\(A:(0.0\mathrm{,0}.0\mathrm{,0}.0)\)

\(B:(1.\mathrm{,0}.0\mathrm{,0}.0)\)

\(C:(1.38\mathrm{,0}.0\mathrm{,0}.0)\)

\(D:(1.5\mathrm{,0}.0\mathrm{,0}.0)\)

1.2. Elastic properties of the material#

  • \(E=2.0E11\mathrm{Pa}\) Young’s module

  • \(\nu =0.3\) Poisson’s ratio

  • \(\rho =7900.0{\mathrm{kg.m}}^{-3}\) Density

1.3. Boundary conditions and loads#

  • Imposed travel:

  • All knots: \(\mathrm{DRX}=\mathrm{DRY}=\mathrm{DX}=\mathrm{DZ}=0.0\)

  • Point \(A\): \(\mathrm{DY}=\mathrm{DRZ}=0.0\)

  • Imposed loading:

  • Point \(B\): random force according to \(Y\)

  • Point \(B\): random moment around \(Z\)

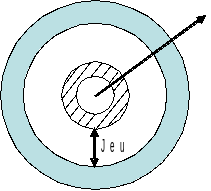
      • Obstacle (CERCLE) at point \(D\):

    • Game = \(0m\)

    • standard = \((1.\mathrm{,0}\mathrm{.}\mathrm{,0}\mathrm{.})\)

    • origin = \((1.\mathrm{,0}\mathrm{.}\mathrm{,0}\mathrm{.})\)

    • Normal stiffness: \(\mathrm{RIGI}\text{\_}\mathrm{NOR}={10}^{6}N/m\)

    • Friction COULOMB: \(\mathrm{COULOMB}=0.3\)

_images/10000200000000D3000000BFD454EEF2F09DD44D.png

      • Obstacle (DISCRET) at point \(C\):

    • standard = \((1.\mathrm{,0}\mathrm{.}\mathrm{,0}\mathrm{.})\)

    • origin = \((1.\mathrm{,0}\mathrm{.}\mathrm{,0}\mathrm{.})\)

    • Normal stiffness: \(\mathrm{RIGI}\text{\_}\mathrm{NOR}=100.N/m\)

    • Friction COULOMB: \(\mathrm{COULOMB}=0.3\)

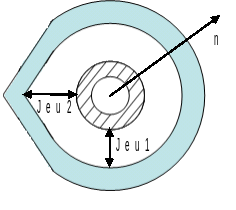
_images/10000200000000EC000000D2D271F1830265DD60.png

    • Game1 = \(1.0m\)

    • Game2 = \(1.5m\)