1. Reference problem#
1.1. Geometry#
We consider the system represented by the diagram below:
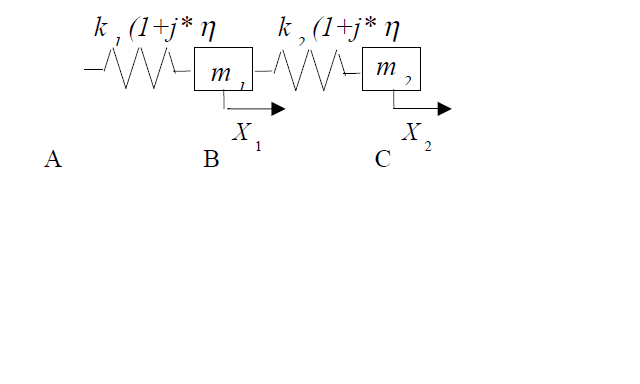
Point masses: |
\({m}_{1}\) and \({m}_{2}\) |
Link stiffness: |
\({k}_{1}\) and \({k}_{2}\) |
Hysteretic damping: |
\({\eta }_{1}\) and \({\eta }_{2}\) |
1.2. Material properties#
Linear elastic translation spring |
\({K}_{1}\mathrm{=}28000N\mathrm{/}m\) |
\({K}_{2}\mathrm{=}28000N\mathrm{/}m\) |
|
Point mass |
\({M}_{1}\mathrm{=}10\mathit{kg}\) |
\({M}_{2}\mathrm{=}5\mathit{kg}\) |
|
Hysteretic damping |
\({\eta }_{1}\mathrm{=}0.1\) |
\({\eta }_{2}\mathrm{=}0.0\) |
1.3. Boundary conditions and loads#
Boundary conditions:
Points \(A\), \(B\), \(C\) embedded in \(\mathit{DY}\) and \(\mathit{DZ}\)
Points \(A\): recessed \((\mathit{DX}\mathrm{=}0)\).
Loading: Sinusoidal concentrated force with variable frequency at point \(C\)
\(\begin{array}{c}{F}_{{x}_{4}}\mathrm{=}{F}_{0}\mathrm{sin}\Omega t\\ \Omega \mathrm{=}2\pi f0\mathit{Hz}\mathrm{\le }f\mathrm{\le }21.0543\mathit{Hz}\\ {F}_{0}\mathrm{=}\mathit{constante}\mathrm{=}\mathrm{100N}\end{array}\)
1.4. Initial conditions#
Not applicable to the study of the permanent harmonic regime.