2. B modeling#
2.1. But#
In this modeling, we want to validate the use of spring mats with zero length DIS_T elements. The feature is already validated for zero-length DIS_TR elements. So that provides the reference values.
2.2. Description#
A structure in the form of a parallelepiped composed of a single element rests on a carpet consisting here of 4 springs. A constant force is imposed on a vertex node of cube \(\mathit{XY}0\) (with components in the 3 directions of space). We then check that the displacement values at node \(\mathit{XY}0\) are the same with modeling DIS_T as with modeling DIS_TR (reference).
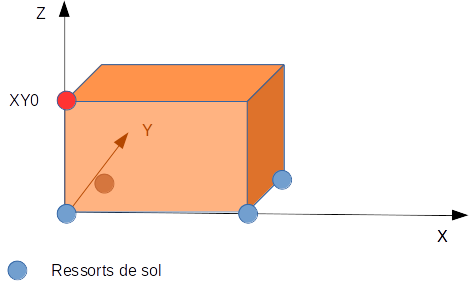
2.2.1. Geometry#
2.2.2. Material parameters#
Structure:
Young’s module: \(30000\mathit{MPa}\)
Poisson’s ratio: \(0.3\)
Density: \(2500\mathit{kg}/{m}^{3}\)
Springs:
GROUP_NO |
Stiffers |
Dampening |
DIS_TR |
1E6,1E6,1E6,2.5E6,2.5E5,2.5E5,5.E5 |
1E3, 1E3, 1E3, 1E3, 2.5E2, 2.5E2, 5.E2 |
DIS_T |
1E6,1E6,1E6 |
1E3,1E3,1E3 |
Note: The rotation values on the DIS_TR given to RIGI_PARASOL in this specific case allow the rotation values to be zero on each element of the spring belt.
2.2.3. Loads#
The following constant forces are imposed on node \(\mathit{XY}0\):
\(\mathit{FX}=1000N\)
\(\mathit{FY}=2000N\)
\(\mathit{FZ}=-3000N\)
2.3. Tested values#
We test the values at the final moment: \(0.5s\)
GROUP_NO |
NUME_ORDRE |
Component |
Reference |
Reference Value |
|
XY0 |
4331 |
|
|
-0.00210267324236 |
|
XY0 |
4331 |
|
|
0.00175325119557 |
|
XY0 |
4331 |
|
|
-0.00691531181833 |