1. Modeling A

1.1. But

The purpose of this test is to validate the use of VMIS_ISOT_TRAC behavior in CALC_EUROPLEXUS.

1.2. Description

The mesh, the model, the elementary characteristics and the loads of the plexu03a test are taken again. Only the material assigned to the elements of BARRE is changed to activate the VMIS_ISOT_TRAC law. Elastic behavior is maintained for the shells.

The elastic properties of materials are recalled:

Material	Concrete	Steel
Young’s module	\({E}_{b}\mathrm{=}{3.0}^{10}\mathit{Pa}\)	\({E}_{a}\mathrm{=}{\mathrm{2.1.10}}^{11}\mathit{Pa}\)
Poisson’s ratio	\({\nu }_{b}\mathrm{=}0.3\)	\({\nu }_{a}\mathrm{=}0.3\)
Density	\({m}_{b}\mathrm{=}2500\mathit{Kg}\mathrm{/}{m}^{3}\)	\({m}_{a}\mathrm{=}7500\mathit{Kg}\mathrm{/}{m}^{3}\)
and the area of the straight section of the cable: :math:`{S}_{a}=mathrm{1	5}{.10}^{-4}{m}^{2}`.

The stress-strain curve induced by the Steel material and the VMIS_ISOT_TRAC behavior is of the following form:

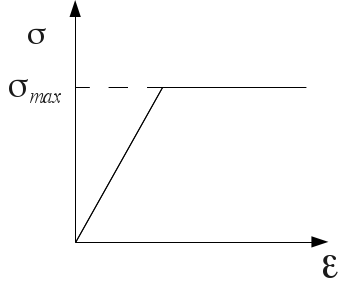
With \({\sigma }_{\mathit{max}}=1E6\).

1.3. Principle of validation

With ELAS behavior across the model, the constraint exceeds the \({\sigma }_{\mathit{max}}\) limit constraint when applying the load. To ensure that law VMIS_ISOT_TRAC is taken into account when executing CALC_EUROPLEXUS, we check that the constraint in the elements of BARRE does not exceed this limit constraint.

To do this, using the keyword COURBE from CALC_EUROPLEXUS, we print the value of the constraint on the 3rd element of BARRE into a table. We then proceed with a TEST_TABLE/TYPE_TEST =” MAX “, to check that the maximum value is indeed the limit constraint.

We also want to validate the good recovery of the internal variables. Of the 5 internal variables of law EPX, only the 3rd component has a direct correspondence in those of Aster. It is therefore necessary to check that this 3rd variable is well placed in the component V1 of VARI_ELGA (EPSPEQ). To do this, using the keyword COURBE, we print the V3 component of the internal variables of the 3rd element of BARRE in the same table as before. We then check with a TEST_RESU that this value is the one found in the VARI_ELGA field of the output result.

Note: the V2 component (INDIPLAS) is left at zero because it is too complicated to rebuild it (it also depends on the time t-1).

1.4. Tested values

The first test is performed on the values from the table, i.e. the values given by EPX without constraint/effort transformation.

Mesh	NUME_ORDRE	Component	Component	Reference Value	Tolerance
SG001003	MAX	\(N\)		“ANALYTIQUE”	106	0.1%
SG001003	100	\(\mathit{V1}\)	“AUTRE_ASTER”	“”	1.6214E-05	0.1%