7. F modeling

In F modeling, we study a 3D structure whose geometry is based on that of the sslv134a test case. We test DEFI_FOND_FISS in the case of a circular closed bottom and a structure with a plane of symmetry.

7.1. Characteristics of the mesh

The mesh and geometry used are those of the sslv134a test case. The mesh is presented by the

next figure:

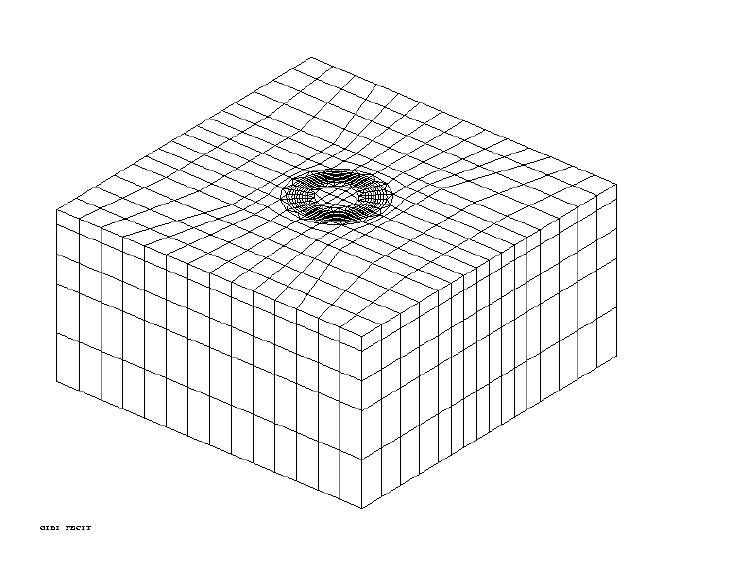
It is composed of 10135 nodes, 1568 solid elements HEXA20 and 864 PENTA15. The closed circular bottom is composed of 65 knots.

7.2. Tested sizes and results

A crack is a circle whose center is the origin of the coordinate system. Thus, the analytical values of the crack propagation direction vectors are the coordinates of the bottom nodes, normalized.

At the bottom node number \(i\) with coordinates \(({\mathit{COORX}}_{i},{\mathit{COORY}}_{i},{\mathit{COORZ}}_{i})\), the crack propagation direction vector is:

\({\mathit{VDIRX}}_{i}\mathrm{=}\frac{{\mathit{COORX}}_{i}}{\sqrt{({\mathit{COORX}}_{i}\mathrm{²}+{\mathit{COORY}}_{i}\mathrm{²}+{\mathit{COORZ}}_{i}\mathrm{²})}}\)

\({\mathit{VDIRY}}_{i}\mathrm{=}\frac{{\mathit{COORY}}_{i}}{\sqrt{({\mathit{COORX}}_{i}\mathrm{²}+{\mathit{COORY}}_{i}\mathrm{²}+{\mathit{COORZ}}_{i}\mathrm{²})}}\)

\({\mathit{VDIRZ}}_{i}\mathrm{=}\frac{{\mathit{COORZ}}_{i}}{\sqrt{({\mathit{COORX}}_{i}\mathrm{²}+{\mathit{COORY}}_{i}\mathrm{²}+{\mathit{COORZ}}_{i}\mathrm{²})}}\)

The vector normal to the crack plane for each of the bottom nodes is carried by the \(z\) axis: \((\mathrm{0,0},\mathrm{-}1)\).

When the crack is defined with a plane of symmetry, the propagation direction vector belongs to the plane of the lip. However, the defined lip is not completely flat. Therefore, the precision of the results is altered along the \(Z\) axis for VDIR and as the normal to the crack plane is calculated from VDIR, the precision of VNORX and/or VNORY is also altered.

For VDIRZ, VNORX and VNORY the percentage of error allowed is 1.8% compared to 1% for the other components.