1. Reference problem

1.1. Geometry

The field studied is stitching: two pipes join together to form a connection. In the example chosen, the aim is to achieve generality by taking different diameters and non-intersecting axes. The geometry is built by Salome. The groups of all edge faces are created. Sharp edge groups are also created.

Each time the mesh is adapted, knots will be created on the edge. If nothing is done, the geometry remains facetted. Here we are testing the ability of HOMARD to replace the new nodes on the curved border.

For 2D borders, the surfaces are described analytically. This is the case of the internal and external faces of the two pipes.

For 1D borders, the lines are described by a very fine ancillary mesh. This is the case of the complex curve that represents the intersection of the two pipes.

For the ends of the cylinders, two scenarios are presented. For the large pipe, the cutting planes are perpendicular to the axis. It is useless to specify the shape of the intersection because the projection onto the cylinder is made in the plane. On the other hand, the external plane of the small pipe is not perpendicular to its axis. It is therefore necessary to describe the curve by means of a fine ancillary mesh.

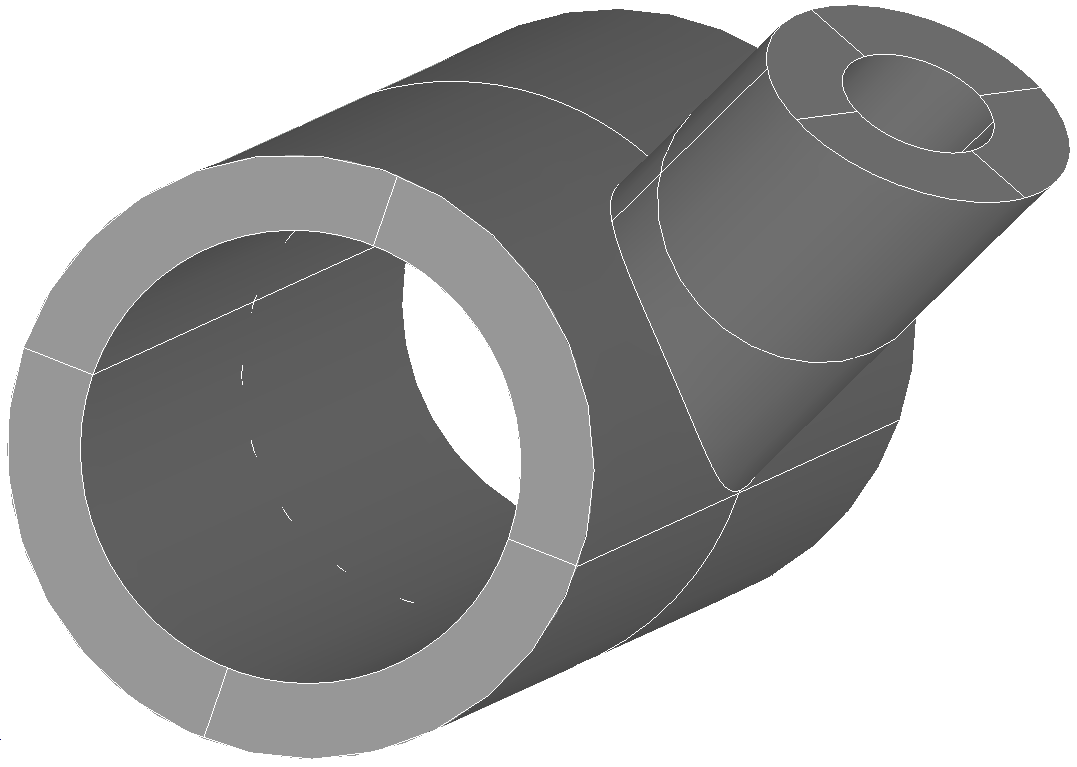
Figure 1.1-1 .: Geometry view

Characteristics:

	Pipe No. 1	Pipe No. 2
\(X\) from the base	0	17.5
\(Y\) from the base	25	-2.5
\(Z\) from the base	-25	-100
\(X\) of the axial vector	25	-100
\(Y\) of the axial vector	50	-75
\(Z\) of the axial vector	75	-25
Inner radius	75	25
Outer radius	100	50
Height	400	250

Table 1.1-2 .: Pipe dimensions

1.2. Material properties

The material is defined with:

Thermal conductivity= \(40{\mathrm{X.m}}^{-{\mathrm{1.K}}^{-1}}\)

1.3. Boundary conditions and loads

The calculation will simulate the thermal state of the pipes in the event that two fluids of different temperatures circulate inside. The outside is placed in the ambient air.

The inside face of the large pipe is blocked at temperature 600.

The inside face of the small pipe is blocked at temperature 400.

The external faces of the two pipes represent a heat exchange with the outside. The exchange coefficient is 5 and the external temperature is equal to 300.

The other external faces on the pipe sections are free. A zero normal flow is deliberately imposed on it, to ensure a correct calculation of the error indicators if one wanted to extend the problem.