1. Reference problem

1.1. Geometry and meshing

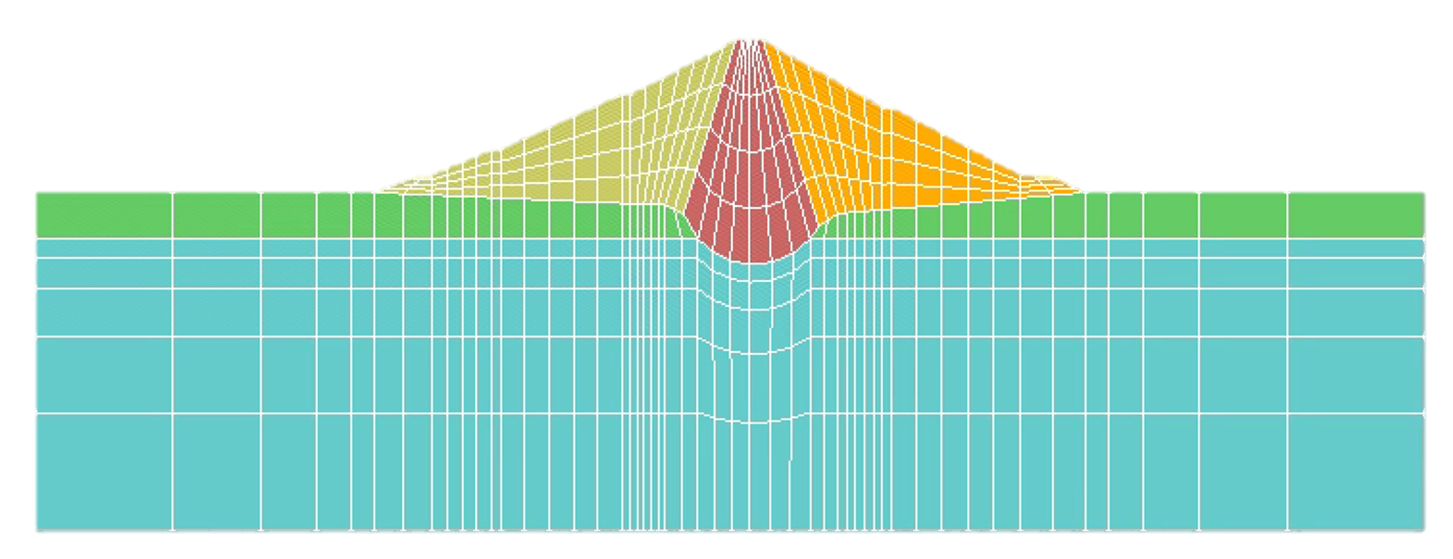
We consider an embankment dam with a clay core, composed of the foundation, gravel between the foundation and the body of the dam, of a clay core characterized by a relatively low permeability coefficient, and backfill refills upstream and downstream.

The mesh is shown in fig1-geom-mail, where the various Components of the dam are shown by different colors.

1.2. Material properties

Table 1: Property of dam materials

The mechanical and hydraulic properties of the materials in the model are shown in Tableau 1.

For the Mohr-Coulomb law, we hypothesize the associated plastic flow law. The parameters of the Drucker-Prager law were obtained by the following formulas:

\(A=\frac{2\mathrm{sin}(\varphi )}{3-\mathrm{sin}(\varphi )},{\sigma }_{y}=\frac{6c\mathrm{cos}(\varphi )}{3-\mathrm{sin}(\varphi )}\)

where the cohesive force and the friction angle take the values in Tableau 1. The angle of expansion is equal to the angle of friction in the Drucker-Prager law.

In order to simplify the calculation, the ultimate cumulative plastic deformation \({p}_{\mathit{ultm}}\) is considered null (= 0).

The porosity is uniform in the model and is equal to 0.672.

1.3. Boundary conditions and loads

The boundary conditions applied to the model are as follows:

• Bottom of the embedded foundation, and the vertical sides normally blocked.

• Hydraulic pressure from the upstream coast of 77.19m (the elevation of the peak = 94.2m).

• Hydraulic pressure defined from the level of the groundwater downstream, which is equal to 43m.

The following mechanical loads are applied to the model:

• Gravity with \(g=\mathrm{9,81}m/{s}^{2}\)

• The hydrostatic pressure on the upper surface of the dam.