4. D modeling#
4.1. Geometry#
This case is a copy of test case SSLV111.
4.2. Boundary conditions and loading#
To represent the symmetries, the part is blocked in normal translation on the cut edges:
Left vertical edge*AB* (group GMP4) :DX = 0
Lower horizontal edge*ED* (group GMP1) :DY = 0
Mechanical loading:
Right vertical edge \(\mathit{CD}\) (group \(\mathit{GMP2}\)): pull ups \(\{\begin{array}{ccc}{F}_{x}& =& {\sigma }_{\mathit{xx}}(x=4.)\\ {F}_{y}& =& {\sigma }_{\mathit{xy}}(x=4.)\end{array}\)
Top horizontal edge \(\mathit{BC}\) (group \(\mathit{GMP3}\)): pull ups \(\{\begin{array}{ccc}{F}_{x}& =& {\sigma }_{\mathit{xy}}(x=4.)\\ {F}_{y}& =& {\sigma }_{\mathit{yy}}(x=4.)\end{array}\)
These constraints are calculated by the analytical solution, described in document [V3.04.111].
The last edge, \(\mathit{AE}\) (group \(\mathit{GMP5}\)), has zero stress.
4.3. Characteristics of the mesh#
The domain is meshed with 11 QUAD4 quadrangles and 1 TRIA3 triangle.
The edges of the domain are meshed into SEG2 segments.
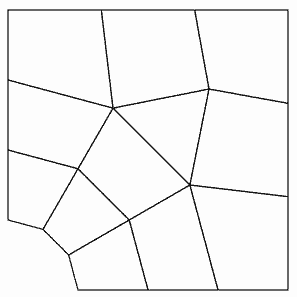
The arc of the curved border is meshed with 300 SEG2. Since they are rectilinear, the other edges are not shown.

4.4. Benchmark results#
The reference is established on the value of the stress field on the two nodes placed on the internal arc, at the angles 30 and 60 degrees. The test is done in non-regression after the first and after the second adaptation. It is compared to the analytical solution after the third adaptation.
30-degree knot |
60-degree knot |
||
Adaptation 1 |
0.8364656 |
1.5763891 |
|
Adaptation 2 |
0.50491074 |
0.50491074 |
1.5891275 |
Adaptation 3 |
0.50830985 |
1.8640630 |
We also test the projection of the field of movement between the 1st and the 2nd adaptation on the 30-degree node: \(\mathit{Ux}=\mathrm{7,733}{10}^{-6}\)