1. Introduction#
Mesh adaptation helps the user to provide calculations that are as reliable as possible with respect to discretization errors due to the finite element method used. Several reasons appear to adapt a network:
meshing is very complicated to produce: we start with a simple version and we entrust an automatic process with the task of refining it.
we want to ensure the convergence of the digital solution: rather than creating ever finer meshes by hand, we let the software look for the places where the mesh should be refined to increase the precision of the result.
the conditions of the calculation change as it is carried out: the areas that must be finely meshed move. If you knit fine everywhere from the start, the mesh is too big. By adapting as you go, the mesh will only be fine in the necessary places: its size will be reduced and the quality of the solution will be good.
Regardless of the software used, the principle of mesh adaptation remains the same. On the initial mesh, the standard calculation is carried out. From an analysis of the numerical solution obtained, we estimate the error that was committed in relation to the real solution. This estimate is represented by an error indicator value in each element of the calculation. From there, the reasoning is simple: the cells where the error indicator is strong should be smaller; conversely, the cells where the error indicator is low could be larger. With this information, we feed the adaptation software, which will modify the mesh accordingly. On the new mesh, the calculation will then be repeated.
Schematically, a mesh adaptation iteration is presented as in the figure below. The software calculates the numerical solution on mesh no. k, then deduces the values of the error indicator on the whole mesh. Based on the knowledge of mesh no. k and the indicator no. k, the mesh adaptation software, HOMARD for Code_Aster, creates the new mesh no. (k+1).
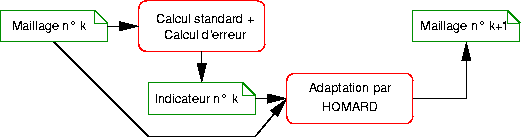
Figure 1-a : Mesh adaptation iteration
For a static calculation, this means seeking to improve the solution by a succession of calculations on different meshes. For a transitory time calculation, the calculation is suspended at a given moment; the mesh is adapted; the calculation is resumed on the new mesh.
With Code_Aster, this adaptation is done by calling an external program, specialized in this task, HOMARD. The purpose of this document is to provide the most complete entry point possible for users who want to implement these types of techniques in their calculations.
The outline of the document is then as follows:
How does HOMARD work;
A focus on error indicators;
A set of tips on « best practices » to implement (what are the points worth paying attention to when using?) ;
A few examples illustrate the use of these techniques and the advice given above (how to do it in practice?).