5. Clean mode post-treatments#
5.1. Visualization#
The modal deformations calculated by one of the methods described above can be exported in various formats in order to be visualized in mechanical calculation platforms: format MED for the Salomé platform, format UNV,…
The user can thus graphically characterize the calculated modes: bending mode? fashion in a given plane? local fashion? etc.
Example:
printed in MED format.
modes = CALC_MODES (…) # modal calculation
IMPR_RESU (FORMAT = “MED”,
RESU =_F (RESULTAT = modes));
We can then open the file created in the Salomé platform to visualize the modal deformation, animate it,…
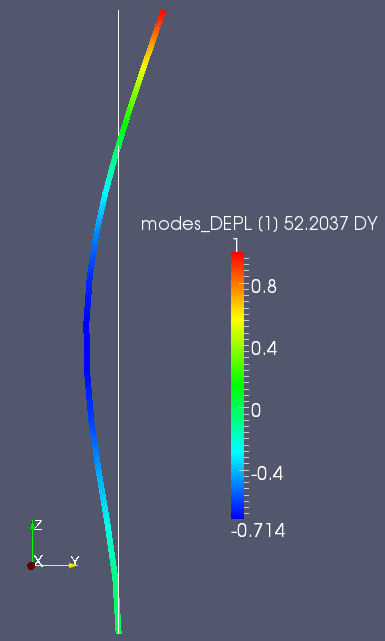
Figure 5.1-a : Visualization of a mode in Salome (ParaVis module): here the 2nd order bending mode of a beam.
5.2. Normalization of modes#
Modal deformations are defined with one multiplicative factor (see formulation of the modal problem in paragraph 1).
By default, the modes calculated by the CALC_MODES operator are normalized so that the largest physical component is equal to 1. The user can modify this normalization, either directly in the operator CALC_MODES using the keyword factor NORM_MODE, or later using the operator NORM_MODE [U4.52.11]. In both cases, the code also calculates or updates the following modal parameters, which depend on the normalization chosen: FACT_PARTICI_D , MASS_GENE, and RIGI_GENE. It also enriches the data structure with the MASS_EFFE_UN_D parameters (which are independent of normalization). These parameters (defined in paragraph 4) can be useful in particular to eliminate certain unwanted modes from a modal basis (see paragraph 5.3).
Example:
norm in relation to mass.
1st possibility:
modes = CALC_MODES (MATR_RIGI = matr_k,
MATR_MASS = matr_m,
OPTION = “BANDE”,
CALC_FREQ =_F (FREQ = (20., 300.)),
NORM_MODE =_F (NORME = “MASS_GENE”)
)
2nd possibility:
modes = CALC_MODES (MATR_RIGI = matr_k,
MATR_MASS = matr_m,
OPTION = “BANDE”,
CALC_FREQ =_F (FREQ = (20., 300.)),
)
modes = NORM_MODE (reuse = modes,
MODE = fashion,
NORME = “MASS_GENE”);
5.3. Filtering modes according to a criterion#
In the perspective of a transient response calculation, for example, the user may choose to keep in his modal projection base, only certain modes considered important in the dynamic response or meeting a given criterion. This can be done either directly in CALC_MODES with the keywords factors FILTRE_MODE and IMPRESSION, or using the EXTR_MODE [U4.52.12] operator. We can thus filter the modes according to various options: from their number in the global spectrum, from their generalized mass, etc.
Example:
elimination of modes whose effective unit mass is less than 5%, and display in file RESULTATdu the cumulative effective unit masses of the retained modes.
1st possibility:
modes = CALC_MODES (MATR_RIGI = matr_k,
MATR_MASS = matr_m,
OPTION = “BANDE”,
CALC_FREQ =_F (FREQ = (20., 300.)),
NORM_MODE =_F (NORME = “MASS_GENE”),
FILTRE_MODE =_F (CRIT_EXTR = “MASS_EFFE_UN”,
SEUIL = 0.05),
IMPRESSION =_F (CRIT_EXTR = “MASS_EFFE_UN”,
CUMUL = “OUI”),
)
2nd possibility:
modes = CALC_MODES (MATR_RIGI = matr_k,
MATR_MASS = matr_m,
OPTION = “BANDE”,
CALC_FREQ =_F (FREQ = (20., 300.)),
NORM_MODE =_F (NORME = “MASS_GENE”),
)
modes_f = EXTR_MODE (FILTRE_MODE =_F (MODE = modes,
CRIT_EXTR = “MASS_EFFE_UN”,
SEUIL = 0.05),
IMPRESSION =_F (CRIT_EXTR = “MASS_EFFE_UN”,
CUMUL = “OUI”),
);
Note:
The operator EXTR_MODE allows you to filter with a threshold applied to one or more given directions (keyword SEUL_Xpar example for the DX direction), which is not possible directly in CALC_MODES currently.