3. Fissure opening#
The crack opening is found by displacement difference \(\mathit{DN}\) in the direction normal to the crack path, between two points \({P}_{g},{P}_{d}\) on this normal.
It is then necessary to determine:
the normal line to the crack path (taking into account the fact that the crack is known discretely by points),
the speed of movements on this line, in particular the component of movement in the same direction,
the coordinates of the two points \({P}_{g},{P}_{d}\) to operate the difference in displacement \(\mathit{DN}\).
The normal is determined on each node in the crack as the bisector of the angle formed by the two normals to the segments that have the node in common (see).
Once normal \(n\) has been determined on a node in the crack path, a change of frame of reference is made in the field of movements, from the global coordinate system to the \((n\mathrm{,}t)\) coordinate system (\(t\) is the tangent vector), in particular the component \(\mathit{DN}\) is calculated.
Points \({P}_{g},{P}_{d}\) are those for which the following relationship is satisfied: \(X\ge\) BORNE_MAX (BORNE_MAX is a parameter to be entered as an operand under the keyword RECHERCHE). The projection of field \(X\ge\) onto the line normal to the path is therefore necessary for the determination of \({P}_{g},{P}_{d}\) (see).
Normally for damage laws, the value \(X\mathrm{=}d\mathrm{=}0.8\) is sufficient to capture the movement jump (see [V1.01.264]).

Figure 4: Average normal to the crack path for the calculation of the crack opening.
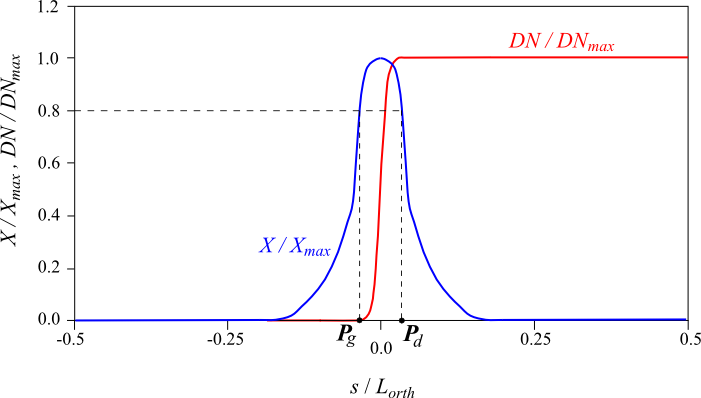
Figure 5: Projection of the DN displacement and the X field onto the normal to the crack path (normalized values); determination of \({P}_{g},{P}_{d}\).