1. Problem position#

The method for calculating stress intensity factors by extrapolation of displacement is based on the asymptotic development of the displacement field at the bottom of a crack.

In 2D, in an elastic, linear, isotropic and homogeneous medium, the stress and displacement fields are known analytically for the modes of opening the crack (characterized by \(\mathit{K1}\)), plane sliding (\(\mathit{K2}\)) and antiplane sliding (\(\mathit{K3}\)), cf. [bib1] and [bib2]. In the general case in 3D, we can show that the asymptotic behavior of displacements and stresses is the sum of the solutions corresponding to modes 1 and 2 (in plane deformations) and to mode 3 (antiplane), and of four other particular solutions, but which are more regular than the previous ones [bib3].

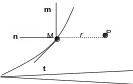
In all cases, the singularity is therefore the same and we can write the following relationships in the normal plane at the bottom of the crack, at point \(M\):

\(\begin{array}{c}{K}_{1}(M)=\underset{r\to 0}{\mathrm{lim}}(\frac{E}{8(1-{\nu }^{2})}[{U}_{m}]\sqrt{\frac{2\pi }{r}})\\ {K}_{2}(M)=\underset{r\to 0}{\mathrm{lim}}(\frac{E}{8(1-{\nu }^{2})}[{U}_{n}]\sqrt{\frac{2\pi }{r}})\\ {K}_{3}(M)=\underset{r\to 0}{\mathrm{lim}}(\frac{E}{8(1+\nu )}[{U}_{t}]\sqrt{\frac{2\pi }{r}})\end{array}\)

with:

\(t,n\)

in the plane of the crack in \(M\)

,

\(t\) vector tangent to the crack bottom in \(M\), \(n\) normal vector at the crack bottom in, vector tangent to the crack bottom in, normal vector at the crack bottom in \(M\) \(m\) vector normal to the plane of the crack in \(M\), \([U]\) displacement jump between the crack lips: \([{U}_{m}]=({U}^{\mathrm{lèvre}\mathrm{supérieure}}-{U}^{\mathrm{lèvre}\mathrm{inférieure}})\cdot m\) \(r=\parallel \text{MP}\parallel\) where \(P\) is a point on the plane normal to the crack bottom in \(M\), located on one of the lips of the crack in, located on one of the lips.

 _images/Shape1.gif

If the crack is not plane, the three vectors are defined locally at point \(M\) of the background in question. The previous relationships therefore provide a method for numerically identifying \(\mathit{K1}\), \(\mathit{K2}\), and \(\mathit{K3}\). From the stress intensity factors, the Irwin formula then makes it possible to calculate the energy return rate \(G\):

\(G=\frac{1}{E}({K}_{1}^{2}+{K}_{2}^{2})\) in plane constraints

\(G=\frac{1-{\nu }^{2}}{E}({K}_{1}^{2}+{K}_{2}^{2})(+\frac{1+\nu }{E}{K}_{3}^{2})\) in plane deformations (and in 3D)

Notes:

**It can be seen that the signs of* \(\mathit{K2}\) and \(\mathit{K3}\) depend on the orientation of \(\text{t}\) and \(\text{n}\). This is not too annoying as the breakage or fatigue criteria only use the absolute values of \(\mathit{K2}\) and \(\mathit{K3}\) .

  • We can also give expressions according to the stress fields, but the values of the vectors constrained on the lips of the crack are less precise than the movements (because they come from a transport from the Gauss points to the nodes) .

  • The expression of asymptotic fields is valid for non-plane cracks (curved cracks for example), but they must still be sufficiently regular. The user must at least ensure that a normal can be defined at any point in the background.

  • The method used here is theoretically less accurate than the calculation using the bilinear form of the energy restoration rate and the singular displacements [R7.02.01 et R7.02.05] (operator CALC_G). However, it makes it easy to obtain relatively reliable values of stress intensity factors. Comparing the various calculation methods is always useful in order to estimate the precision of the results obtained.