2. Implementation of extrapolation methods#

The methods for extrapolating displacements are implemented in operator POST_K1_K2_K3, based on the displacement field calculated over the entire structure. The definitions of stress intensity factors are only true asymptotically; extrapolation is therefore carried out by restricting itself to the vicinity of the crack bottom limited by a maximum distance \(\mathit{dmax}\) to the bottom. \(\mathit{dmax}\) is the ABSC_CURV_MAXI operator parameter. In the case of a mesh crack ABSC_CURV_MAXI is optional. If it is not graded, \(\mathit{dmax}\) is automatically calculated in POST_K1_K2_K3 and is worth four times the maximum size of the meshes connected to the nodes in the background.

The general principle of the calculation is as follows:

Loop on the node at the bottom of the crack (current point: \(M\))

Definition of plane \(\Gamma\) normal to the crack and to the bottom of the crack, at point \(M\) (normal plane \(\text{t}\))

Identifying the knots on both lips that belong to \(\Gamma\): \({P}_{i}^{\text{sup}}\) and \({P}_{i}^{\text{inf}}\)

Loop on these knots:

If \({r}_{i}^{\text{sup}}=\parallel {\text{MP}}_{i}^{\text{sup}}\parallel \text{dmax}\): extraction of the displacement in \({P}_{i}^{\text{sup}}\)

If \({r}_{i}^{\text{inf}}=\parallel {\text{MP}}_{i}^{\text{inf}}\parallel \text{dmax}\): extraction of the displacement in \({P}_{i}^{\text{inf}}\)

Calculation of the displacement jump in the three directions

Extrapolation of the displacement jump

Three extrapolation methods are programmed. They are illustrated in this paragraph for a meshed crack (quadratic mesh), with or without « Barsoum » elements. The Barsoum elements are such that the non-vertex nodes on the sides of the quadratic elements touching the bottom of the crack are moved to a quarter of the [bib4] side. They make it possible to better capture the singularity of the stress field at the bottom of the crack.

_images/Object_27.png

Classic finite element (M being a cleft node)

 _images/Object_28.png

Finite element of the Barsoum type

  • Method 1: we calculate the jump in the displacement field squared and divide it by \(r\). Different values of \({K}^{2}\) are obtained (with one multiplying factor) by extrapolating the line segments thus obtained to \(r\mathrm{=}0\). If the solution was perfect (asymptotic analytic field everywhere), we should get a line. In reality, we almost get a line with a « Barsoum » type mesh, and a non-straight curve otherwise:

_images/Object_30.svg

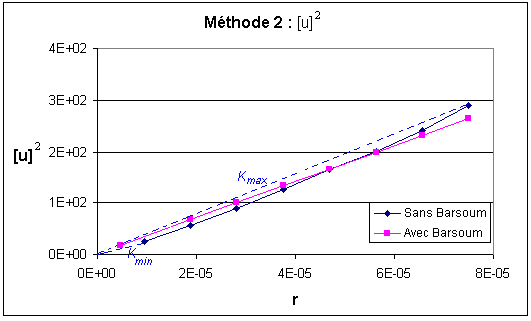
  • Method 2: we plot the jump in the squared displacement field according to \(r\). The approximations to \(K\) are (always with one multiplying factor) equal to the root of the slope of the segments connecting the origin to the various points of the curve.

_images/Object_32.png

  • Method 3: we identify the stress intensity factor \(K\) from the displacement jump \(\mathrm{[}U\mathrm{]}\) using a least squares method. The adjustment is done on a segment of length \(\mathit{dmax}\), where \(\mathit{dmax}\) is the parameter fixed in the parameter set in the operand ABSC_CURV_MAXI of the POST_K1_K2_K3 operator or in the case of a mesh crack, if ABSC_CURV_MAXI is not indicated, \(\mathit{dmax}\) is equal to four times the maximum size of the cells connected to the nodes in the background:

\(K\) minimizes \(J(k)=\frac{1}{2}\underset{0}{\overset{\text{dmax}}{\int }}{([U(r)]-k\sqrt{r})}^{2}\mathrm{dr}\)

So let’s be the explicit formula to calculate \(K\):

\(K=\frac{2}{{r}_{m}^{2}}\underset{0}{\overset{\text{dmax}}{\int }}[U(r)]\sqrt{r}\mathrm{dr}=\frac{1}{{r}_{m}^{2}}\sum _{i=0}^{\mathrm{nbno}-1}({r}_{i+1}-{r}_{i})({[U]}_{i+1}\sqrt{{r}_{i+1}}-{[U]}_{i}\sqrt{{r}_{i}})\)

where \(\mathit{nbno}\) is the number of nodes on the \(\mathrm{[}\mathrm{0,}\mathit{dmax}\mathrm{]}\) realignment segment. Note that in this expression \(K\) is, for a fixed \(\mathit{dmax}\), a linear form of the displacement field.