2. Theoretical formulation#
2.1. State variables, state law#
The state variables are: total deformation \(\mathrm{\epsilon }\left(\mathrm{u}\right)\), plastic deformation \({\mathrm{\epsilon }}^{p}\).
Free energy density is written as:
where \(\mathrm{A}\) refers to the linear elasticity tensor; it is assumed to be isotropic (2 independent elastic coefficients in 3D). Work hardening is not considered.
The elastoplastic three-dimensional law of behavior is then written (state law):
2.2. Criterion (load area) smoothed#
The criterion delimiting the elastic domain (load surface) is formulated with the 3 tensor invariants:
with \({I}_{1}=\text{tr}\left(\mathrm{\sigma }\right)=3p\) the triple of the mean pressure, \({J}_{2}=\frac{1}{2}\left({\mathrm{\sigma }}^{D}\mathrm{:}{\mathrm{\sigma }}^{D}\right)=\frac{1}{3}{\left({\Vert \mathrm{\sigma }\Vert }_{\mathit{VM}}\right)}^{2}\); \({J}_{3}=\text{det}\left({\mathrm{\sigma }}^{D}\right)\), having noted \({\mathrm{\sigma }}^{D}=\mathrm{\sigma }-p\mathrm{Id}\) the stress tensor deviator, and the modified Lode angle defined by: \({\theta }_{L}=\frac{1}{3}\mathrm{arcsin}\left(\text{-}\frac{3\sqrt{3}{J}_{3}}{2\sqrt{{J}_{2}^{3}}}\right)\phantom{\rule{2em}{0ex}}\in \phantom{\rule{2em}{0ex}}\left[\text{-}\frac{\pi }{6},\frac{\pi }{6}\right]\), and the three parameters: cohesion \(c\), the friction angle \({\varphi }_{\mathit{pp}}\), and the « traction truncation » \({a}_{\mathit{tt}}\), which is used for the approximation hyperbolic used for smoothing at the top of the Mohr-Coulomb pyramid. cf. [2].
Note 1 :
According to [2 ], if \({a}_{\mathit{tt}}=0\) , criterion (3) finds the top of the pyramid of Mohr-Coulomb, so it is no longer smoothed. if Si*:math:{a}_{mathit{tt}}=frac{1}{2}cmathrm{.}mathit{cotan}{varphi }_{mathit{pp}}`*, * ** *then at the top of the smoothed criterion, we check:* :math:`{I}_{1}=0 .
We know that the main constraints can be written according to:
: label: eq-4
{begin {array} {c} {sigma} {sigma} _ {I} _ {1} {1} +frac {2sqrt {3}}} {3}} {3}mathrm {.} sqrt {{J} _ {2}}}mathrm {.} mathrm {sin}left ({theta} _ {L} _ {L} +frac {2pi} {3}right)\ {sigma} _ {mathit {II}}} =frac {1}}}} =frac {1}} _ {1} +frac {2sqrt {3}} {3}}mathrm {.} sqrt {{J} _ {2}}}mathrm {.} mathrm {sin}left ({theta} _ {L}right)\ {L}right)\ {sigma} _ {mathit {III}}} =frac {1} {3} {3} {3} {3} {3} {3} {3} {3} {I} _ {1} {1} {I} _ {1}} +frac {1} _ {1} +frac {1} _ {1} +frac {1} _ {1} +frac {1} _ {1} +frac {1} _ {1} +frac { sqrt {{J} _ {2}}}mathrm {.} mathrm {sin}left ({theta} _ {L} -frac {2pi} {3}right)end {array}
The \(K\left({\theta }_{L}\right)\) function in (3) is defined by:
: label: eq-5
Kleft ({theta} _ {L}right) ={begin {array} {cc} {left (mathrm {cos} {theta} _ {L} -frac {sqrt {3}}right) ={sqrt {3}} {sqrt {3}} {3}}mathrm {3}} {3}mathrm {3}} {3}mathrm {3}} {3}mathrm {3}} {3}mathrm {3}} {3}mathrm {3}} {3}mathrm {3}} {3}mathrm {.} mathrm {sin} {theta} _ {L}right)}} ^ {2}}} ^ {2} &mathit {si}phantom {rule {2em} {0ex}}left| {theta}} _ {L}\ right} _ {L}\ right|< {L}right|< {L}right|< {L}right|< {theta} | right|< {theta} | right|< {theta} | right|< {theta} | right|< {theta} | right|< {theta} | right|< {theta} | right|< {theta} | right|< {theta} | right|< {theta}} | right|<left ({theta} _ {L}right)mathrm {.} mathrm {sin} 3 {theta} _ {L} _ {L} +Cleft ({theta} _ {L}right)mathrm {.} {mathrm {sin}} ^ {2} 3 {theta} _ {L}right)} ^ {2} &mathit {si}phantom {rule {2em} {0ex}}left| {theta}}}left| {theta}}}left| {theta} _ {theta} _ {T}end {array}}}left| {theta}}}left| {theta} _ {theta} _ {array}
with an additional \({\theta }_{T}\in \phantom{\rule{2em}{0ex}}\left[0,\frac{\pi }{6}\right]\) parameter called transition angle and \(A\left({\theta }_{L}\right),B\left({\theta }_{L}\right),C\left({\theta }_{L}\right),\) functions defined by:
Note 2 :
According to [2 ], we should not take a value of \({\theta }_{T}\) too close to \(\frac{\pi }{6}\) , at the risk of poor conditioning; and a typical value of \({\theta }_{T}\) can be taken equal to \(\frac{5\pi }{36}\). With this value of . With this value of \({\theta }_{T}\) and with \({a}_{\mathit{tt}}=\frac{1}{20}c\mathrm{.}\mathit{cotan}{\varphi }_{\mathit{pp}}\) , the proposed hyperbolic smoothing leads to an error of at most 0.13% in The plan deviatory from the original Mohr-Coulomb pyramid.
The and are a graphical representation of the original Mohr-Coulomb load surface in the principal stress space. The shows the effect of smoothing [2] on the edges of the Mohr-Coulomb charge surface.
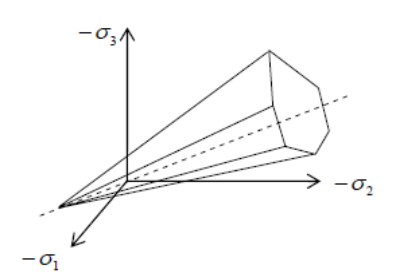
Figure 2.2-1: Representation of the Mohr-Coulomb load surface in the three-dimensional space of the main stresses.
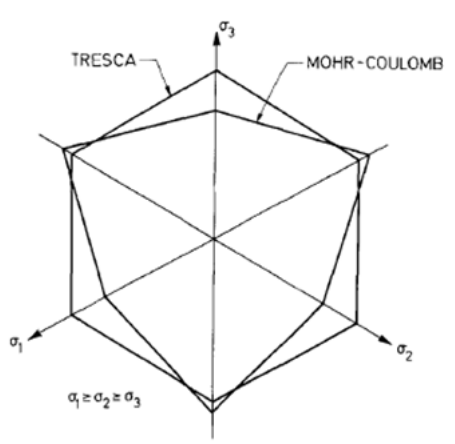
Figure 2.2-2: Representation of the Mohr-Coulomb load surface in plane \(\mathrm{\pi }\) of the stress deviators (any vector represented in this plane corresponds to a deviatoric stress).
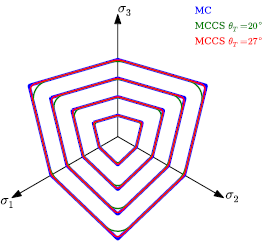
Figure 2.2-3: Representation of the Mohr-Coulomb load surface smoothed in plane \(\pi\) of the stress deviators, for the friction angle \({\varphi }_{\mathit{pp}}=25°\) and two values of \({\theta }_{T}\) (taken from [3]).
An enrichment of the criterion () is provided by adding a term for hardening to cohesion, in the following form:
where the parameter \({r}_{\mathit{eg}}\) (expressed without units) makes it possible to introduce linear cohesion work hardening.
2.3. Plastic flow potential#
The plastic flow of this law is not standard (non-associated law), and therefore not oriented according to the normal to the load surface. The authors [2] propose an expression of plastic flow using another potential with the same analytical form as that of the criterion (), by involving the dilatance angle \(\psi\):
When \(\psi ={\varphi }_{\mathit{pp}}\), the law of plastic flow becomes associated.
Function \({K}_{g}\left({\theta }_{L}\right)\) in (7) is defined by:
functions \({A}_{\text{g}}\left({\theta }_{L}\right),{B}_{\text{g}}\left({\theta }_{L}\right),{C}_{\text{g}}\left({\theta }_{L}\right),\) being defined by:
When the stress state is on load surface \(\text{f}\left(\mathrm{\sigma }\right)=0\), the plastic deformation rate is normal to potential \(\text{g}\left(\mathrm{\sigma }\right)\) and is written with the plastic multiplier \(d\lambda\):
where the normal tensor of order two outside the surface is:
The only true thermodynamic internal variable is the equivalent plastic deformation \({\Vert {\epsilon }^{p}\Vert }_{\mathit{VM}}\).
We naturally have \(\frac{\partial \text{g}\left(\sigma \right)}{\partial {I}_{1}\left(\sigma \right)}=\frac{1}{3}\cdot \mathrm{sin}\psi\) and we remind you that: \(\frac{\partial {J}_{2}\left(\sigma \right)}{\partial \sigma }={\sigma }^{D}\).
Note 3 :
L e flow potential chosen, in the same shape as the criterion, therefore the flow tensor of flow \({\mathrm{n}}_{\text{g}}\) , is not affected by the possible introduction of linear cohesion work hardening, cf. * () () *. In fact, the evolution of cohesion does not modify the direction normal to the faces of the pyramid \(\text{g}\left(\mathrm{\sigma }\right)=0\) .
2.4. Energy dissipation by plastic flow#
The mechanical power density dissipated by the plasticity mechanism is:
Mechanical energy is dissipated by accumulation during the loading path.
2.5. Behavioral relationship parameters#
The parameters of the behavioral relationship are:
YoungModulus |
Young’s Modulus (positive) |
\(E\) |
PoissonRatio |
Poisson Ratio |
\(\nu\) |
Cohesion |
Cohesion (positive or zero) |
\(c\) |
FrictionAngle |
Friction angle (supplied in°) |
\({\varphi }_{\mathit{pp}}\) |
dilatancyAngle |
Expansion angle (supplied in°) |
\(\psi\) |
TransitionAngle |
Transition Lode Angle (supplied in°, less than 30°) |
\({\theta }_{T}\) |
TensionCutoff |
Traction truncation (positive or zero) |
\({a}_{\mathit{tt}}\) |
HardeningCoef |
Cohesion hardening (positive or zero) |
\({r}_{\mathit{eg}}\) |