2. Formulation in terms of main constraints#
This formulation is only valid under the hypothesis of isotropy of the material [,]. Indeed, this condition is necessary to ensure that the radial return method preserves the main directions. Its interest lies in the fact that it simplifies the writing of equations and therefore allows very efficient (because they are almost analytical) resolution methods.
The elastic behavior is purely linear.
The load surface is characterized by six planes in the space of the main stresses \(\left({\sigma }_{1},{\sigma }_{2},{\sigma }_{3}\right)\). Each of these planes is characterized by an equation of the type:
Where \(\phi\) and \(c\) are material data and characterize the internal friction angle and the cohesion of the material respectively.
The law is not associated and the plastic flow potential \({G}_{13}\) associated with the charge surface \({F}_{13}\) is written in the same way:
Where \(\psi\) is a material data and characterizes the angle of expansion of the material.
When \(\psi =\varphi\), the law of plastic flow becomes associated.
A graphical representation of the Mohr-Coulomb load surface in the principal stress space is in the figure and in the plane \(\pi\) in the figure.
It is observed that the six planes intersect two by two along an angular edge, and meet at the top of the cone characterized by the equation:
These edges, of which there are six, as well as the top of the cone, form singularities that pose problems of numerical integration, because the derivatives of the charge surface are not defined at these locations. Methods for resolving this difficulty will be discussed later.

Figure 2-1: Representation of the Mohr-Coulomb load surface in the three-dimensional space of the principal stresses
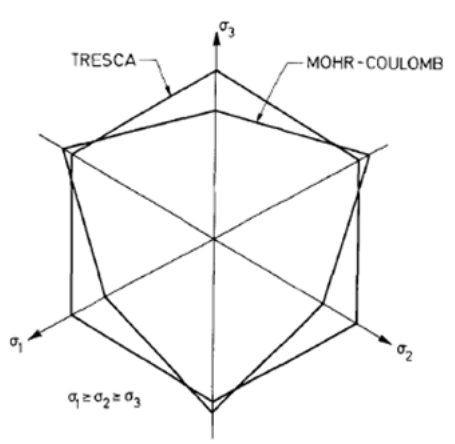
Figure 2-2: Representation of the Mohr-Coulomb load surface in plane \(\pi\) of the stress deviators (any vector represented in this plane corresponds to a deviatory stress).