1. Presentation of the BETON_REGLE_PR law#
The law of behavior is of the « twice 1D » type in the natural deformation coordinate system (confused with the natural stress coordinate system). We only describe a 1D behavior, which is of the non-linear elastic type.
In compression, it is the law rectangular parabola defined by regulations [bib1]; the constraint is given by the following relationships:
In traction the law is of the triangle type [bib2]:
The associated material parameters are as follows:
\(E\): Young’s modulus;
\({\sigma }_{y}^{t}\): the peak tensile stress (\({f}_{t}\));
\({E}_{T}\): the tangent module (generally between \(\frac{\mathrm{-}E}{3}\) and \(\frac{\mathrm{-}E}{10}\));
\({\sigma }_{y}^{c}\): the maximum compression stress (\({f}_{c}\));
\(n\): the exponent of the law of work hardening in compression;
\({\varepsilon }_{c}\): the deformation at which \({\sigma }_{y}^{c}\) is reached.
The stress-strain response is given in the following figure:
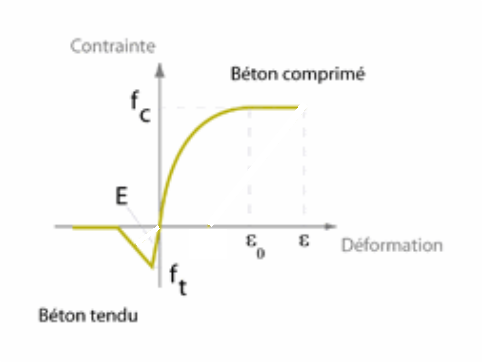
Figure 1-a : 1D stress-strain curve
In order for the original slopes in tension and in compression to be identical, the parameters can be chosen in such a way that: