3. Modeling of touch/friction by penalization

3.1. Normal contact force model

The principle of penalization applied to the graph in the figure consists in introducing an unequivocal relationship \({F}_{N}^{1/2}={f}_{\mathrm{ϵ}}\left({d}_{N}^{1/2}\right)\) by means of a parameter \(\varepsilon\). The \({f}_{\varepsilon }\) graph should tend towards the Signorin graph when \(\varepsilon\) tends to zero (see [2]). One of the possibilities is to propose a linear relationship between \({d}_{N}^{1/2}\) and \({F}_{N}^{1/2}\):

(3.1)\[ \ {\ begin {array} {c} {F} _ {F} _ {N} _ {N} {d} _ {N} ^ {1/2}\ text {si} {d}\ text {si} {d} _ {d} _ {N} {d} _ {N} {d} _ {N} ^ {1/2} =0\ text {else} ^ {1/2}\ text {otherwise}\ text {d} {d}}\ text {d} {d} _ {n} ^ {1/2}\ text {if} {1/2}\ text {si} {d}}\ text {d} {d}} _ {n} ^ {1/2}\ text {si} {d}}\ text {d} {d} _ {n} ^ {1/2}\ text {si} {d}\\]

If we note \({K}_{N}=\frac{1}{\mathrm{ϵ}}\) (commonly called shock stiffness) we find the classical relationship, modeling an elastic shock:

(3.2)\[ {F} _ {N} ^ {1/2} =- {K} _ {N} {d} _ {N} ^ {1/2} =- {K} _ {N} ^ {1/2}\]

The approximate graph of the law of contact with penalization is in the figure.

Figure 3-1: Graph of the unilateral contact relationship approximated by penalization

To take into account a possible loss of energy in the shock, shock absorption \({C}_{N}\) is introduced. The expression for the normal contact force is then expressed as:

(3.3)\[ {F} _ {N} ^ {1/2} =- {K} =- {K} _ {N} {d} _ {N} ^ {1/2} - {C} _ {N} _ {N}} {\ dot {u}}} _ {N} ^ {1/2}\]

Where \({\dot{u}}_{N}^{1/2}\) is the relative normal speed of \({O}_{1}\) compared to \({O}_{2}\). To respect the Signorin relationship (no adhesion in contact), on the other hand, we must check afterwards whether \({F}_{N}^{1/2}\) is positive or zero. So we will only take the positive part \({⟨\cdot ⟩}^{+}\) of the expression ():

(3.4)\[\begin{split} \ {\ begin {array} {c} {⟨x⟩}} ^ {+}} ^ {+} =x\ text {si} x\ ge 0\\ {⟨x⟩}} ^ {+} =0\ text {x} =0\ text {si} x<0\ end {array}\end{split}\]

The complete relationship giving the normal contact force that is retained for the algorithm is as follows:

(3.5)\[\begin{split} \ {\ begin {array} {c}\ text {If} {d} _ {N} {d} _ {N}} ^ {1/2}\ le 0\ text {then} {F} _ {N} {K} _ {N} {K} _ {N} {d} _ {n} {d} _ {n} {K} _ {N} {K} _ {K} _ {K} _ {K} _ {K} _ {K} _ {N} {K} _ {K} _ {N} {K} _ {K} _ {N} {K} _ {K} _ {N} {K} _ {K} _ {N} _ {K} _ {N} {K} _ {K} _ {N} _ {K} _ {N} {K} _ {K} _ {text {+}}\ text {and} {F} _ {N} _ {N} ^ {1/2} =- {F} _ {N} ^ {2/1}\\ text {Else} {F} _ {F} _ {N} _ {F}} _ {1/2} = {F} _ {N} ^ {2/1} =0\ end {array} _ {1} = 0\ end {array}\end{split}\]

3.2. Tangential contact force model

The graph describing the tangential force with Coulomb’s law is non-differentiable for the adhesion phase \({\dot{u}}_{T}^{1/2}=0\). A univocal relationship is therefore introduced linking the relative tangential displacement \({d}_{T}^{1/2}\) and the tangential force \({F}_{T}^{1/2}={f}_{\mathrm{\xi }}\left({d}_{T}^{1/2}\right)\) by means of a parameter \(\xi\). The \({f}_{\xi }\) graph should tend towards the Coulomb graph when \(\xi\) tends to zero (see [2]). One of the possibilities is to write a linear relationship between \({d}_{T}^{1/2}\) and \({F}_{T}^{1/2}\) for incremental writing:

(3.6)\[ {F} _ {T} ^ {1/2} - {F} _ {F} _ {T\ mathrm {,0}}} ^ {1/2} =-\ frac {1} {\ mathrm {\ xi}}\ left ({d} _ {D} _ {D}} _ {T\ mathrm {,0}}} {\ mathrm {\ xi}}}\ left ({d}}}\ left ({d} _ {d}}\ left ({d} _ {D}}\ right)\]

With \({\left(\cdot \right)}_{T\mathrm{,0}}\) the quantities at the previous time step. If we introduce a tangential stiffness \({K}_{T}=\frac{1}{\mathrm{\xi }}\), we get the relationship:

(3.7)\[ {F} _ {T} ^ {1/2} = {F} _ {F} _ {T\ mathrm {,0}}} ^ {1/2} - {K} _ {T} _ {T} {T} ^ {1/2} - {1/2} - {d} - {d} _ {D} _ {T\ mathrm {,0}}} ^ {1/2}\ right)\]

The approximate graph of Coulomb’s law of friction modeled by penalization is in the figure. For numerical reasons, linked to the dissipation of parasitic vibrations (see [3]) during the adhesion phase, it is necessary to add tangential damping \({C}_{T}\) in the expression of the tangential force. Its final expression is:

(3.8)\[ {F} _ {T} ^ {1/2} = {F} _ {F} _ {F} _ {F} _ {1/2}} - {K} _ {T} _ {T} ^ {1/2} - {1/2} - {d} - {d} - {d} _ {d} _ {d} _ {D} _ {T}} - {T}} _ {T}} - {T}} - {T}} - {T}} - {T}} - {T}} - {T}} - {T}} - {T}} - {T}} - {T}} - {T}} - {T}} - {T}} - {T}} - {T}} 1/2}\]

In addition, this force must satisfy the Coulomb criterion, namely:

(3.9)\[ \ Green {F} _ {T} ^ {1/2}\ Green\ le\ mathrm {\ mu} {F} _ {N} ^ {1/2} ^ {1/2}\]

If this is not the case, the frictional force is corrected by the following formula:

(3.10)\[ {F} _ {T} ^ {1/2} =-\ mathrm {\ mu} {F} {F} _ {N} ^ {1/2}\ frac {{\ dot {u}} _ {T} ^ {1/2}} {\ 1/2}}} {\ green {\ 1/2}}} {\ green} {\ green} {\ green}} {\ green}\]

Figure 3-2: Graph of the law of friction approximated by penalization

In the case of the extension of Coulomb’s law with the distinction between the adhesion coefficient \({\mu }_{s}\) and the sliding coefficient \({\mu }_{d}\), the approximate graph of the law is modified (see figure).

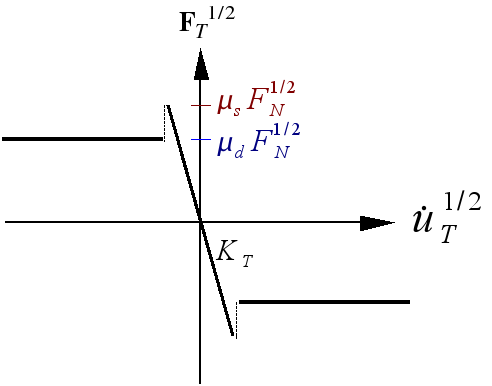
Figure 3-3: Graph of the variant of the law of friction approximated by penalization