4. Determination of the equivalent stiffness of the crack

4.1. Equivalent crack model

In this chapter, we seek to determine the law of behavior \(M=f([\theta ])\) relating, for the 1D crack element, the bending forces \(M\) to the deformations expressed by the jump in rotation \([\theta ]=\left(\begin{array}{c}[{\theta }_{y}(x)]\\ [{\theta }_{z}(x)]\end{array}\right)\) of the crack lips represented by the two border nodes of the crack represented by the two border nodes of the crack.

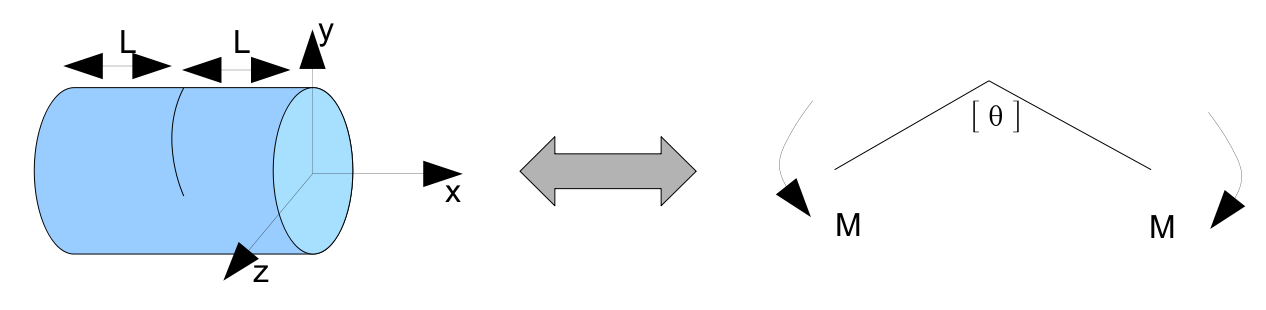
4.2. Deformation energy

4.2.1. Formula for deformation energy at imposed force

In [1] we establish that the energy of the 3D model in a near static state is given by a « Clapeyron » formula:

\({W}^{f}({M}_{y},{M}_{z})=\frac{1}{2}\left({M}_{y}{\theta }_{y}(\mathrm{2L})+{M}_{z}{\theta }_{z}(\mathrm{2L})\right)\)

On the 3D finite element model, using this formula, we can calculate the energy of the system for all possible torques \(({M}_{y},{M}_{z})\) and determine the equivalent stiffness \(k({M}_{y},{M}_{z})\) for the 1D element of a cracked beam.

However, exploring a space equivalent to \({ℝ}^{2}\) would be too expensive for practical application. The properties of the energy functional of the elastic problem with contact make it possible to reduce the problem to a single variable.

We show that \({W}^{f}\) is convex and positively homogeneous of degree 2 with respect to the moments applied:

\(\forall \lambda \ge 0,{W}^{f}(\lambda {M}_{y},\lambda {M}_{z})={\lambda }^{2}{W}^{f}({M}_{y},{M}_{z})\)

This property is interesting because it means, in practice, that the contact zone on the lips of the crack is independent of the amplitude \(M\) of the flexure. The energy is quadratic in \(M\), as in the linear case. Its shape only depends on the direction of \(({M}_{y},{M}_{z})\). We can therefore rewrite the energy function with, as variables, the magnitude of the flexural force \(\mid \mid M\mid \mid\) and its angle \(\phi\).

In the cylindrical coordinate system the moment is written:

\(\begin{array}{c}{M}_{y}=\mid \mid M\mid \mid \mathrm{cos}\varphi \\ {M}_{z}=\mid \mid M\mid \mid \mathrm{sin}\varphi \end{array}\) and the deformation energy: \({W}_{f}(M)=\frac{1}{2}{\mid \mid M\mid \mid }^{2}S(\varphi )\)

The problem is reduced to identifying \(S(\phi )\) on the \([\mathrm{0,}2\pi ]\) interval.

Energy is rewritten in a form that distinguishes flexibility \(S(\varphi )\), provided by the beams (healthy and cracked parts) and flexibility \(s(\phi )\), provided by the crack:

\({W}^{f}(M)=\frac{L}{\mathit{EI}}{\mid \mid M\mid \mid }^{2}(1+s(\varphi ))\)

By calculating the deformation energy on a 3D finite element model of the cracked bar (figure), we can determine \(s(\varphi )\).

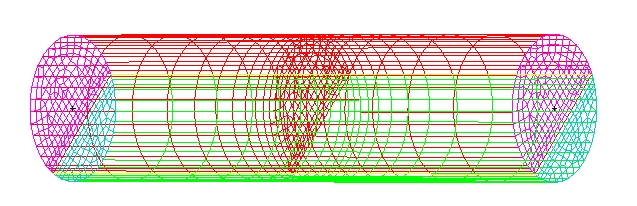
Illustration 1:3D mesh of the cracked bar

4.2.2. Imposed displacement energy

Now it remains to establish the relationship between energy and \([\theta ]\). Imposed displacement energy \({w}^{d}\) is used for this. It has the same convexity and homogeneity properties of degree 2 as energy at imposed effort.

By posing:

\(\begin{array}{c}[{\theta }_{x}]=\mid \mid [\theta ]\mid \mid \mathrm{cos}(\phi )\\ [{\theta }_{y}]=\mid \mid [\theta ]\mid \mid \mathrm{sin}(\phi )\end{array}\)

the following expression is obtained for the deformation energy:

\({w}^{d}([\theta ])=\frac{\mathit{EI}}{\mathrm{4L}}{\mid \mid [\theta ]\mid \mid }^{2}k(\phi )\)

4.2.3. Law of behavior of the cracked element

We get \(M\) as a function of \(\mathrm{[}\theta \mathrm{]}\) by deriving the energy:

\(\begin{array}{c}{M}_{y}\mathrm{=}\frac{\mathit{EI}}{\mathrm{4L}}\frac{\mathrm{\partial }(k(\varphi )({\mathrm{[}{\theta }_{y}\mathrm{]}}^{2}+{\mathrm{[}{\theta }_{z}\mathrm{]}}^{2}))}{\mathrm{\partial }{\mathrm{[}\theta \mathrm{]}}_{y}}\\ {M}_{z}\mathrm{=}\frac{\mathit{EI}}{\mathrm{4L}}\frac{\mathrm{\partial }(k(\varphi )({\mathrm{[}{\theta }_{y}\mathrm{]}}^{2}+{\mathrm{[}{\theta }_{z}\mathrm{]}}^{2}))}{\mathrm{\partial }{\mathrm{[}\theta \mathrm{]}}_{z}}\end{array}\) with \(\mathrm{[}\theta \mathrm{]}\mathrm{=}\sqrt{{\mathrm{[}{\theta }_{y}\mathrm{]}}^{2}+{\mathrm{[}{\theta }_{z}\mathrm{]}}^{2}}(\begin{array}{c}\mathrm{cos}(\varphi )\\ \mathrm{sin}(\varphi )\end{array})\)

Some intermediate calculations lead to the following relationships:

\(\left(\begin{array}{c}{M}_{y}\\ {M}_{z}\end{array}\right)=\frac{\mathit{EI}}{\mathrm{2L}}\left(\begin{array}{c}k(\phi )-\frac{1}{2}k\text{'}(\phi )\\ \frac{1}{2}k\text{'}(\phi )k(\phi )\end{array}\right)\left(\begin{array}{c}[{\theta }_{y}(x)]\\ [{\theta }_{z}(x)]\end{array}\right)\) where \(\varphi \mathrm{=}\mathrm{arctan}(\frac{\mathrm{[}{\theta }_{z}(x)\mathrm{]}}{\mathrm{[}{\theta }_{y}(x)\mathrm{]}})\)

4.2.4. Relationship between crack stiffness and crack opening angle

The \(\phi\) direction of the mean opening angle of the crack \([\theta ]\) is*a priori* not the same as \(\phi\), that of the efforts of the moments \(M\).

It is therefore now a question of establishing a direct relationship between stiffness (or its opposite, flexibility) and the opening of the crack. It is established in [1] and [2].

By exploiting the principle of complementary energy and thanks to the convexity of the deformation energy, it is shown that:

\({w}^{d}(\mathrm{[}\theta \mathrm{]})\mathrm{=}\underset{M}{\mathit{Sup}}(\mathit{M.}\mathrm{[}\theta \mathrm{]}\mathrm{-}\frac{L}{\mathit{EI}}{\mathrm{\mid }\mathrm{\mid }M\mathrm{\mid }\mathrm{\mid }}^{2}s(\phi ))\)

The \(s(\phi )\) function has been established in the preceding paragraphs. An additional mathematical treatment consists in applying to \(s(\phi )\) a quadratic interpolation outside the null interval of \(s(\phi )\) and a power interpolation to the nullity limits of \(s(\phi )\).

Moreover, in the same way as the energy at the imposed moment, the energy at imposed deformation is convex and homogeneous of order 2. This implies that it does not depend on the \(\mathrm{[}\theta \mathrm{]}\) standard, but only on its \(\varphi\) direction. So we can limit ourselves to identifying \({w}^{d}(\mathrm{[}\theta \mathrm{]})\) for \(\mathrm{\mid }\mathrm{\mid }\mathrm{[}\theta \mathrm{]}\mathrm{\mid }\mathrm{\mid }\mathrm{=}1\).

Energy is then written:

\({w}^{d}(\mathrm{[}\theta \mathrm{]})\mathrm{=}\frac{\mathit{EI}}{\mathrm{4L}}k(\varphi )\).

If \(\lambda\) is the magnitude of the moment applied and \(\phi\) is its direction, by identification we find the formula giving the equivalent crack stiffness:

\(k(\varphi )\mathrm{=}\frac{\mathrm{4L}}{\mathit{EI}}\underset{M\mathrm{=}1}{\mathit{Sup}}\underset{\lambda \mathrm{\ge }0}{\mathit{Sup}}(\lambda \mathit{M.}\mathrm{[}\theta \mathrm{]}\mathrm{-}\frac{L}{\mathit{EI}}{\lambda }^{2}s(\phi ))\)

In practice, this amounts to finding the domain \(\mathrm{[}{\varphi }_{\mathrm{1,}}{\varphi }_{2}\mathrm{]}\) that the direction of the crack may have and then maximizing the following expression for all possible crack angles \(\varphi\):

\(k(\varphi )\mathrm{=}\underset{\phi \mathrm{\in }\mathrm{[}\varphi \mathrm{-}\frac{\pi }{\mathrm{2,}}\varphi +\frac{\pi }{2}\mathrm{]}}{\mathit{Sup}}\frac{{\mathrm{cos}}^{2}(\phi \mathrm{-}\varphi )}{s(\phi )}\)

The derivative \(k\text{'}(\varphi )\mathrm{=}\frac{dk(\varphi )}{d\varphi }\) is then obtained using a Finite Difference derivation of \(k(\varphi )\).