2. Choice of finite elements

The introduction of new nodal variables requires the use of elements compatible with the new formulation. We are faced with three nodal unknowns: the movements \(u\), the regularized variable \(\alpha\) and the Lagrange multiplier \(\lambda\).

Since the internal variable field is linked to the deformations through the criterion, it is preferable to take the same degree of interpolation for the regularized internal variable field \(\alpha\) as for the deformation, that is to say a degree less than the displacements from which the deformations are derived. The same degree of interpolation is chosen for the Lagrange multiplier \(\lambda\) as for the regularized variable \(\alpha\).

We therefore consider functions of forms \({P}^{2}\) for \(u\), \({P}^{1}\) for \(\alpha\) and \({P}^{1}\) for \(\lambda\)

The quadratic elements, TRIA6 and QUAD8 for 2D, TETRA10, PENTA15 and HEXA20 for 3D, have been developed. The displacement components are assigned to all the nodes of the element while the components of the other two nodal variables are only assigned to the vertex nodes. For greater clarity, element TRIA6 is shown below:

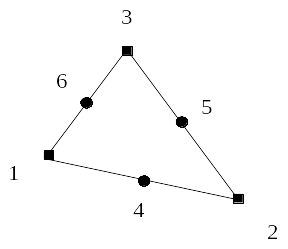
The families of Gauss points of the corresponding linear elements are used, which results in under-integration on the movements. Using the families of Gauss points for quadratic elements would involve over-integration for \(\alpha\) and \(\lambda\), causing untimely oscillations.