4. Numerical discretization of variational formulations

4.1. Discretization of displacement fields and deformation fields for the beam part

At a point on the middle fiber, the beam displacement field is in the local curvilinear coordinate system defined in [§2.1]: \({U}^{p}=(\begin{array}{}{u}_{x}\\ {u}_{y}\\ {u}_{z}\\ {\theta }_{x}\\ {\theta }_{y}\\ {\theta }_{z}\end{array})\)

This field can be discretized in the following way:

\(u=\sum _{k=1}^{N}{H}_{k}(\theta )[{u}_{x}^{k}{x}_{k}+{u}_{y}^{k}{y}_{k}+{u}_{z}^{k}{z}_{k}]\) and \(\theta =\sum _{k=1}^{N}\overline{{H}_{k}}(\theta )[{\theta }_{x}^{k}{x}_{k}+{\theta }_{y}^{k}{y}_{k}+{\theta }_{z}^{k}{z}_{k}]\)

Note that the nodal values are given in the local coordinates attached to the nodes and that \(u\) and \(\theta\) must be expressed in the local coordinate system associated with the current point.

4.1.1. Curved beam

We then obtain:

\((\begin{array}{c}{u}_{x}\\ {u}_{y}\\ {u}_{z}\end{array})=\sum _{k=1}^{N}{H}_{k}(\theta )(\begin{array}{c}{u}_{x}^{k}({x}_{k}\text{.}x)+{u}_{y}^{k}({y}_{k}\text{.}x)\\ {u}_{x}^{k}({x}_{k}\text{.}y)+{u}_{y}^{k}({y}_{k}\text{.}y)\\ {u}_{z}^{k}{z}_{k}\end{array})\) and \((\begin{array}{c}{\theta }_{x}\\ {\theta }_{y}\\ {\theta }_{z}\end{array})=\sum _{k=1}^{N}{\stackrel{ˉ}{H}}_{k}(\theta )(\begin{array}{c}{\theta }_{x}^{k}({x}_{k}\text{.}x)+{\theta }_{y}^{k}({y}_{k}\text{.}x)\\ {\theta }_{x}^{k}({x}_{k}\text{.}y)+{\theta }_{y}^{k}({y}_{k}\text{.}y)\\ {\theta }_{z}^{k}{z}_{k}\end{array})\)

According to the beam kinematics shown above in [§2.1]:

\(\begin{array}{}{\varepsilon }_{\text{rr}}=0\\ {\varepsilon }_{\theta \theta }=\frac{1}{R+r\text{sin}\phi }({u}_{x,\theta }-{u}_{y}-r{\theta }_{x}\text{cos}\phi +{\theta }_{z,\theta }r\text{sin}\phi -{\theta }_{y,\theta }r\text{cos}\phi )\\ {\varepsilon }_{\phi \phi }=0\\ 2{\varepsilon }_{\theta \phi }=\frac{1}{R+r\text{sin}\phi }(-{u}_{x}\text{cos}\phi -{u}_{y,\theta }\text{cos}\phi +{u}_{z,\theta }\text{sin}\phi -r{\theta }_{x,\theta }+{\theta }_{y}r{\text{cos}}^{2}\phi -{\theta }_{z}r\text{sin}\phi \text{cos}\phi )\\ +({\theta }_{z}\text{cos}\phi +{\theta }_{y}\text{sin}\phi )\\ 2{\varepsilon }_{r\theta }=\frac{1}{R+r\text{sin}\phi }(-{u}_{x}\text{sin}\phi -{u}_{y,\theta }\text{sin}\phi -{u}_{z,\theta }\text{cos}\phi +{\theta }_{y}r\text{sin}\phi \text{cos}\phi -{\theta }_{z}r{\text{sin}}^{2}\phi )\\ +({\theta }_{z}\text{sin}\phi -{\theta }_{y}\text{cos}\phi )\\ 2{\varepsilon }_{r\phi }=0\end{array}\)

Knowing that \({x}_{,\theta }=-y\) and \({y}_{,\theta }=x\) plus \(x\text{.}{x}_{k}=y\text{.}{y}_{k}=\text{cos}(\theta -{\theta }_{k})={C}_{k}\text{et}y\text{.}{x}_{k}=-x\text{.}{y}_{k}=\text{sin}(\theta -{\theta }_{k})={S}_{k}\).

For the deformation field, this implies:

\(\begin{array}{}{\varepsilon }_{\theta \theta }=\frac{1}{R+r\text{sin}\phi }\sum _{k=1}^{N}[{H}_{k}^{\text{'}}({u}_{x}^{k}\text{cos}(\theta -{\theta }_{k})-{u}_{y}^{k}\text{sin}(\theta -{\theta }_{k}))+{H}_{k}(-{u}_{x}^{k}\text{sin}(\theta -{\theta }_{k})-{u}_{y}^{k}\text{cos}(\theta -{\theta }_{k}))\\ -{H}_{k}({u}_{x}^{k}\text{sin}(\theta -{\theta }_{k})+{u}_{y}^{k}\text{cos}(\theta -{\theta }_{k}))-r{\stackrel{ˉ}{H}}_{k}\text{cos}\phi ({\theta }_{x}^{k}\text{cos}(\theta -{\theta }_{k})-{\theta }_{y}^{k}\text{sin}(\theta -{\theta }_{k}))\\ -r{\stackrel{ˉ}{H}}_{k}^{\text{'}}\text{cos}\phi ({\theta }_{x}^{k}\text{sin}(\theta -{\theta }_{k})+{\theta }_{y}^{k}\text{cos}(\theta -{\theta }_{k}))-r{\stackrel{ˉ}{H}}_{k}\text{cos}\phi ({\theta }_{x}^{k}\text{cos}(\theta -{\theta }_{k})-{\theta }_{y}^{k}\text{cos}(\theta -{\theta }_{k}))\\ +r{\stackrel{ˉ}{H}}_{k}^{\text{'}}\text{sin}\phi {\theta }_{z}^{k}]\\ {\varepsilon }_{\phi \phi }=0\\ {\gamma }_{\theta \phi }=\sum _{k=1}^{N}\frac{1}{R+r\text{sin}\phi }[-{H}_{k}\text{cos}\phi ({u}_{x}^{k}\text{cos}(\theta -{\theta }_{k})-{u}_{y}^{k}\text{sin}(\theta -{\theta }_{k}))\\ -{H}_{k}^{\text{'}}\text{cos}\phi ({u}_{x}^{k}\text{sin}(\theta -{\theta }_{k})+{u}_{y}^{k}\text{cos}(\theta -{\theta }_{k}))-{H}_{k}\text{cos}\phi ({u}_{x}^{k}\text{cos}(\theta -{\theta }_{k})-{u}_{y}^{k}\text{sin}(\theta -{\theta }_{k}))\\ +{H}_{k}^{\text{'}}{u}_{z}^{k}\text{sin}\phi -r{\stackrel{ˉ}{H}}_{k}^{\text{'}}({\theta }_{x}^{k}\text{cos}(\theta -{\theta }_{k})-{\theta }_{y}^{k}\text{sin}(\theta -{\theta }_{k}))-r{\stackrel{ˉ}{H}}_{k}(-{\theta }_{x}^{k}\text{sin}(\theta -{\theta }_{k})-{\theta }_{y}^{k}\text{cos}(\theta -{\theta }_{k}))\\ +r{\stackrel{ˉ}{H}}_{k}{\text{cos}}^{2}\phi ({\theta }_{x}^{k}\text{sin}(\theta -{\theta }_{k})+{\theta }_{y}^{k}\text{cos}(\theta -{\theta }_{k}))-r{\stackrel{ˉ}{H}}_{k}{\theta }_{z}^{k}\text{sin}\phi \text{cos}\phi ]\\ +{\stackrel{ˉ}{H}}_{k}\text{sin}\phi ({\theta }_{x}^{k}\text{sin}(\theta -{\theta }_{k})+{\theta }_{y}^{k}\text{cos}(\theta -{\theta }_{k}))+{\stackrel{ˉ}{H}}_{k}{\theta }_{z}^{k}\text{cos}\phi \\ {\gamma }_{r\theta }=\sum _{k=1}^{N}\frac{1}{R+r\text{sin}\phi }[-{H}_{k}\text{sin}\phi ({u}_{x}^{k}\text{cos}(\theta -{\theta }_{k})-{u}_{y}^{k}\text{sin}(\theta -{\theta }_{k}))\\ -{H}_{k}^{\text{'}}\text{sin}\phi ({u}_{x}^{k}\text{sin}(\theta -{\theta }_{k})+{u}_{y}^{k}\text{cos}(\theta -{\theta }_{k}))-{H}_{k}\text{sin}\phi ({u}_{x}^{k}\text{cos}(\theta -{\theta }_{k})-{u}_{y}^{k}\text{sin}(\theta -{\theta }_{k}))\\ -{H}_{k}^{\text{'}}{u}_{z}^{k}\text{cos}\phi +r{\stackrel{ˉ}{H}}_{k}\text{sin}\phi \text{cos}\phi ({\theta }_{x}^{k}\text{sin}(\theta -{\theta }_{k})+{\theta }_{y}^{k}\text{cos}(\theta -{\theta }_{k}))-r{\stackrel{ˉ}{H}}_{k}{\theta }_{z}^{k}{\text{sin}}^{2}\phi ]\\ -{\stackrel{ˉ}{H}}_{k}\text{cos}\phi ({\theta }_{x}^{k}\text{sin}(\theta -{\theta }_{k})+{\theta }_{y}^{k}\text{cos}(\theta -{\theta }_{k}))+{\stackrel{ˉ}{H}}_{k}{\theta }_{z}^{k}\text{sin}\phi \end{array}\)

Or in matrix form:

\((\begin{array}{c}{\varepsilon }_{\theta \theta }^{P}\\ {\gamma }_{\theta \phi }^{P}\\ {\gamma }_{\theta \zeta }^{P}\end{array})=\sum _{k=1}^{N}{B}_{k}^{P}{U}_{k}^{P}\) where \({U}_{k}^{p}=(\begin{array}{}{u}_{x}^{k}\\ {u}_{y}^{k}\\ {u}_{z}^{k}\\ {\theta }_{x}^{k}\\ {\theta }_{y}^{k}\\ {\theta }_{z}^{k}\end{array})\) is the move field at node \(k\)

and

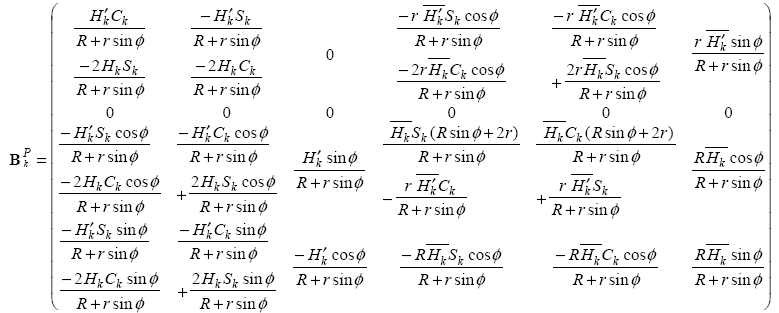
The matrix for the transition from deformations to the field of displacement is written as follows: \({B}^{P}=({B}_{{}^{1}}^{P}\cdots {B}_{{}^{N}}^{P})\)

4.1.2. Right beam

\((\begin{array}{}{u}_{x}\\ {u}_{y}\\ {u}_{z}\end{array})=\sum _{k=1}^{N}{H}_{k}(x)(\begin{array}{}{u}_{x}^{k}\\ {u}_{y}^{k}\\ {u}_{z}^{k}\end{array})\) and \((\begin{array}{}{\theta }_{x}\\ {\theta }_{y}\\ {\theta }_{z}\end{array})=\sum _{k=1}^{N}\stackrel{ˉ}{{H}_{k}}(x)(\begin{array}{}{\theta }_{x}^{k}\\ {\theta }_{y}^{k}\\ {\theta }_{z}^{k}\end{array})\)

According to the beam kinematics shown above [§2.1]:

\(\begin{array}{}{\varepsilon }_{\text{rr}}=0\\ {\varepsilon }_{\text{xx}}={u}_{x,x}+{\theta }_{z,x}r\text{sin}\phi -{\theta }_{y,x}r\text{cos}\phi \\ {\varepsilon }_{\phi \phi }=0\\ 2{\varepsilon }_{x\phi }=-r{\theta }_{x,x}+({\theta }_{y}+{u}_{z,x})\text{sin}\phi +({\theta }_{z}-{u}_{y,x})\text{cos}\phi \\ 2{\varepsilon }_{\text{rx}}=({\theta }_{z}-{u}_{y,x})\text{sin}\phi -({\theta }_{y}+{u}_{z,x})\text{cos}\phi \\ 2{\varepsilon }_{r\phi }=0\end{array}\)

for the deformation field, this implies:

\(\begin{array}{}{\varepsilon }_{\text{xx}}=\sum _{k=1}^{N}({H}_{k}^{\text{'}}{u}_{x}^{k}-{\overline{{H}^{\text{'}}}}_{k}r\text{cos}(\phi ){\theta }_{y}^{k}+{\overline{{H}^{\text{'}}}}_{k}r\text{sin}(\phi ){\theta }_{z}^{k})\\ {\varepsilon }_{\phi \phi }=0\\ {\gamma }_{\mathrm{x\phi }}=\sum _{k=1}^{N}(-{H}_{k}^{\text{'}}\text{cos}(\phi ){u}_{y}^{k}+{H}_{k}^{\text{'}}\text{sin}(\phi ){u}_{z}^{k}-{\overline{{H}^{\text{'}}}}_{k}r{\theta }_{x}^{k}+{\overline{H}}_{k}\text{sin}(\phi ){\theta }_{y}^{k}+{\overline{H}}_{k}\text{cos}(\phi ){\theta }_{z}^{k})\\ {\gamma }_{\text{rx}}=\sum _{k=1}^{N}(-{H}_{k}^{\text{'}}\text{sin}(\phi ){u}_{y}^{k}-{H}_{k}^{\text{'}}\text{cos}(\phi ){u}_{z}^{k}-{\overline{H}}_{k}\text{cos}{(\phi )}_{y}^{k}+{\overline{H}}_{k}\text{sin}(\phi ){\theta }_{z}^{k})\end{array}\)

Or in matrix form:

\((\begin{array}{c}{\varepsilon }_{x}^{P}\\ {\varepsilon }_{\phi }^{P}\\ {\gamma }_{x\phi }^{P}\\ {\gamma }_{x\zeta }^{P}\end{array})=\sum _{k=1}^{N}{B}_{k}^{P}{U}_{k}^{P}\) where \({U}_{k}^{p}=(\begin{array}{}{u}_{x}^{k}\\ {u}_{y}^{k}\\ {u}_{z}^{k}\\ {\theta }_{x}^{k}\\ {\theta }_{y}^{k}\\ {\theta }_{z}^{k}\end{array})\) is the move field at node \(k\)

and:

\({B}_{{}^{k}}^{P}=(\begin{array}{cccccc}{H}_{k}^{\text{'}}& 0& 0& 0& -r\text{cos}(\phi )\overline{{H}_{k}^{\text{'}}}& r\text{sin}(\phi )\overline{{H}_{k}^{\text{'}}}\\ 0& 0& 0& 0& 0& 0\\ 0& -\text{cos}(\phi ){H}_{k}^{\text{'}}& \text{sin}(\phi ){H}_{k}^{\text{'}}& -r\overline{{H}_{k}^{\text{'}}}& \text{sin}(\phi )\overline{{H}_{k}}& \text{cos}(\phi )\overline{{H}_{k}}\\ 0& -\text{sin}(\phi ){H}_{k}^{\text{'}}& -\text{cos}(\phi ){H}_{k}^{\text{'}}& 0& -\text{cos}(\phi )\overline{{H}_{k}}& \text{sin}(\phi )\overline{{H}_{k}}\end{array})\)

The matrix for the transition from deformations to the field of displacement is written as follows: \({B}^{P}=({B}_{{}^{1}}^{P}\cdots {B}_{{}^{N}}^{P})\)

4.2. Discretization of the displacement and deformation fields for the additional part

We discretize the displacement field for the surface of the pipe in the form: \({U}^{s}=\sum _{k=1}^{N}{H}_{k}(x){U}_{k}^{s}\) with:

\({U}^{s}=\left[\begin{array}{c}{u}_{m}^{i}\\ {v}_{m}^{i}\\ {w}_{m}^{i}\\ {u}_{m}^{o}\\ {v}_{m}^{o}\\ {w}_{m}^{o}\\ {w}_{1}^{i}\\ {w}_{1}^{o}\\ {w}_{}^{o}\end{array}\right]\) and. \({U}_{k}^{s}=\left[\begin{array}{c}{u}_{\mathrm{km}}^{i}\\ {v}_{\mathrm{km}}^{i}\\ {w}_{\mathrm{km}}^{i}\\ {u}_{\mathrm{km}}^{o}\\ {v}_{\mathrm{km}}^{o}\\ {w}_{\mathrm{km}}^{o}\\ {w}_{\mathrm{k1}}^{i}\\ {w}_{\mathrm{k1}}^{o}\\ {w}_{k}^{o}\end{array}\right]\) \(\begin{array}{}\\ \\ \\ \\ \\ \\ \\ \end{array}\}m=\mathrm{2,}M\)

We thus have:

\(\begin{array}{}(\begin{array}{c}u(x,\phi )\\ v(x,\phi )\\ w(x,\phi )\end{array})=(\begin{array}{cccccccccc}\text{cos}(m\phi )& 0& 0& \text{sin}(m\phi )& 0& 0& ⋮& 0& 0& 0\\ 0& \text{sin}(m\phi )& 0& 0& \text{cos}(m\phi )& 0& ⋮& \text{sin}(\phi )& -\text{cos}(\phi )& 0\\ 0& 0& \text{cos}(m\phi )& 0& 0& \text{sin}(m\phi )& ⋮& \text{cos}(\phi )& \text{sin}(\phi )& 1\end{array}){U}^{s}\\ \\ m=\mathrm{2,}M\end{array}\)

if the \(m\) indices of \({U}_{k}^{s}\) are ordered as follows:

\({U}_{k}^{s}=(\begin{array}{c}{u}_{km=2}^{i}\\ {v}_{km=2}^{i}\\ {w}_{km=2}^{i}\\ {u}_{km=2}^{o}\\ {v}_{km=2}^{o}\\ {w}_{km=2}^{o}\\ ⋮\\ {u}_{km=M}^{i}\\ {v}_{km=M}^{i}\\ {w}_{km=M}^{i}\\ {u}_{km=M}^{o}\\ {v}_{km=M}^{o}\\ {w}_{km=M}^{o}\\ {w}_{k1}^{i}\\ {w}_{k1}^{o}\\ {w}_{k}^{o}\end{array})\)

The shell kinematics presented above in [§2.2] is:

\(\begin{array}{}{\varepsilon }_{\theta \theta }={E}_{\theta }+\zeta {\kappa }_{x}\\ {\varepsilon }_{\phi \phi }={E}_{\phi }+\zeta {\kappa }_{\phi }\\ {\gamma }_{\theta \phi }=2{E}_{\theta \phi }+2\zeta {\kappa }_{\theta \phi }\\ {\gamma }_{\theta \zeta }=2{E}_{\theta \zeta }=0\\ {\gamma }_{\phi \zeta }=2{E}_{\phi \zeta }=0\end{array}\)

4.2.1. Coude

With:

\(\begin{array}{}{E}_{\theta \theta }=\frac{1}{R+r\text{sin}\phi }(\frac{\partial u}{\partial \theta }+v\text{cos}\phi +w\text{sin}\phi )\\ {E}_{\phi \phi }=\frac{1}{r}(\frac{\partial v}{\partial \phi }+w)\\ 2{E}_{\theta \phi }=\frac{1}{r}\frac{\partial u}{\partial \phi }+\frac{1}{R+r\text{sin}\phi }(\frac{\partial v}{\partial \theta }-u\text{cos}\phi )\end{array}\)

and:

\(\begin{array}{}{\kappa }_{\theta \theta }=\frac{1}{R+r\text{sin}\phi }[-\frac{1}{R+a\text{sin}\phi }(\frac{{\partial }^{2}w}{\partial {\theta }^{2}}-\frac{\partial u}{\partial \theta }\text{sin}\phi )-\frac{\text{cos}\phi }{a}(\frac{\partial w}{\partial \phi }-v)]\\ {\kappa }_{\phi \phi }=-\frac{1}{\text{ar}}(\frac{{\partial }^{2}w}{\partial {\phi }^{2}}-\frac{\partial v}{\partial \phi })\\ 2{\kappa }_{\theta \phi }=(\frac{\partial w}{\partial \theta }-u\text{sin}\phi )[\frac{\text{cos}\phi }{(R+r\text{sin}\phi )(R+a\text{sin}\phi )}+\frac{a\text{cos}\phi }{r(R+a\text{sin}\phi {)}^{2}}]\\ -\frac{{\partial }^{2}w}{\partial \theta \partial \phi }[\frac{1}{a(R+r\text{sin}\phi )}+\frac{1}{r(R+a\text{sin}\phi )}]\\ +\frac{\partial v}{\partial \theta }\frac{1}{a(R+r\text{sin}\phi )}+(\frac{\partial u}{\partial \phi }\text{sin}\phi +u\text{cos}\phi )\frac{1}{r(R+a\text{sin}\phi )}\end{array}\)

makes it possible to decompose the shell deformation field on Fourier modes in the following way:

\((\begin{array}{c}{\varepsilon }_{\text{xx}}^{s}\\ {\varepsilon }_{\phi \phi }^{s}\\ {\gamma }_{x\phi }^{s}\\ {\gamma }_{x\zeta }^{s}\end{array})=\sum _{k=1}^{N}{B}_{k}^{s}{U}_{k}^{s}\) with:

\({B}_{k}^{s}=(\begin{array}{ccccccc}{B}_{km=2}^{\text{si}}& \cdots & {B}_{km=M}^{\text{si}}& {B}_{km=2}^{\text{so}}& \cdots & {B}_{km=M}^{\text{so}}& {B}_{k}^{\text{sg}}\end{array})\)

where

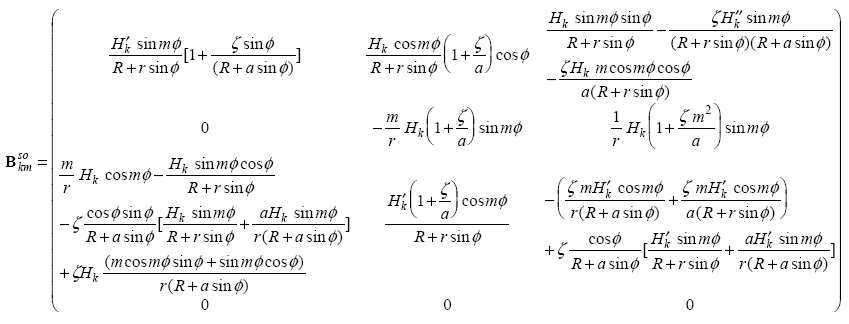
and

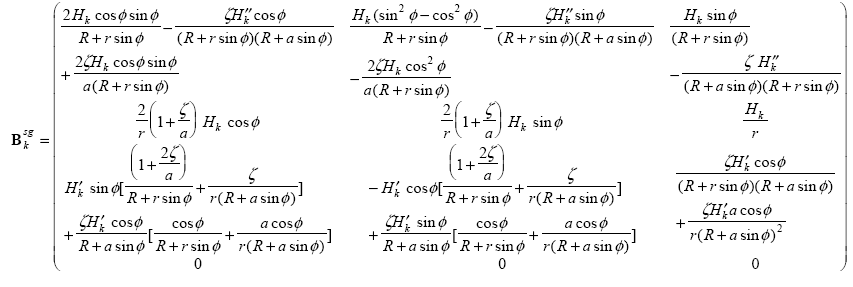
4.2.2. Straight pipe

With:

\(\begin{array}{}{E}_{\text{xx}}=\frac{\partial u}{\partial x}\\ {E}_{\text{φφ}}=\frac{1}{r}(\frac{\partial v}{\partial \phi }+w)\\ 2{E}_{\mathrm{x\phi }}=\frac{\partial v}{\partial x}+\frac{1}{r}\frac{\partial u}{\partial \phi }\\ {\kappa }_{\text{xx}}=\frac{\partial {\beta }_{\phi }}{\partial x}\\ {\kappa }_{\text{φφ}}=-\frac{1}{a}\frac{\partial {\beta }_{x}}{\partial \phi }\\ 2{\kappa }_{\mathrm{x\phi }}=\frac{1}{r}\frac{\partial {\beta }_{\phi }}{\partial \phi }-\frac{\partial {\beta }_{x}}{\partial x}\end{array}\)

\(\begin{array}{}{\beta }_{\phi }=-\frac{\partial w}{\partial x}\\ {\beta }_{x}=\frac{1}{a}(\frac{\partial w}{\partial \phi }-v)\end{array}\)

the shell deformation field is decomposed on Fourier modes as follows:

\(\begin{array}{}{\epsilon }_{\text{xx}}=\frac{\partial }{\partial x}\sum _{n=1}^{N}\sum _{m=2}^{M}{H}_{n}(x)(\text{cos}{\mathrm{m\phi u}}_{\text{nm}}^{i}+\text{sin}{\mathrm{m\phi u}}_{\text{nm}}^{o})\\ -\zeta \frac{{\partial }^{2}}{\partial {x}^{2}}\sum _{n=1}^{N}{H}_{n}(x)\left[{w}_{n}^{o}+\sum _{m=1}^{M}(\text{cos}{\mathrm{m\phi w}}_{\text{nm}}^{i}+\text{sin}{\mathrm{m\phi w}}_{\text{nm}}^{o})\right]\\ {\epsilon }_{\text{φφ}}=\frac{1}{r}\frac{\partial }{\partial \phi }\sum _{n=1}^{N}{H}_{n}(x)\left[\text{sin}{\mathrm{\phi w}}_{\mathrm{n1}}^{i}-\text{cos}{\mathrm{\phi w}}_{\mathrm{n1}}^{o}+\sum _{m=2}^{M}(\text{sin}{\mathrm{m\phi v}}_{\text{nm}}^{i}+\text{cos}{\mathrm{m\phi v}}_{\text{nm}}^{o})\right]\\ +\frac{1}{r}\sum _{n=1}^{N}{H}_{n}(x)\left[{w}_{n}^{o}+\sum _{m=1}^{M}(\text{cos}{\mathrm{m\phi w}}_{\text{nm}}^{i}+\text{sin}{\mathrm{m\phi w}}_{\text{nm}}^{o})\right]\\ +\frac{\zeta }{ar}\frac{\partial }{\partial \phi }\sum _{n=1}^{N}{H}_{n}(x)\left[\text{sin}{\mathrm{\phi w}}_{\mathrm{n1}}^{i}-\text{cos}{\mathrm{\phi w}}_{\mathrm{n1}}^{o}+\sum _{m=2}^{M}(\text{sin}{\mathrm{m\phi v}}_{\text{nm}}^{i}+\text{cos}{\mathrm{m\phi v}}_{\text{nm}}^{o})\right]\\ -\frac{\zeta }{ar}\frac{{\partial }^{2}}{\partial {\phi }^{2}}\sum _{n=1}^{N}{H}_{n}(x)\left[{w}_{n}^{o}+\sum _{m=1}^{M}(\text{cos}{\mathrm{m\phi w}}_{\text{nm}}^{i}+\text{sin}{\mathrm{m\phi w}}_{\text{nm}}^{o})\right]\\ {\gamma }_{\mathrm{x\phi }}=\frac{\partial }{\partial x}\sum _{n=1}^{N}{H}_{n}(x)\left[\text{sin}{\mathrm{\phi w}}_{\mathrm{n1}}^{i}-\text{cos}{\mathrm{\phi w}}_{\mathrm{n1}}^{o}+\sum _{m=2}^{M}(\text{sin}{\mathrm{m\phi v}}_{\text{nm}}^{i}+\text{cos}{\mathrm{m\phi v}}_{\text{nm}}^{o})\right]\\ +\frac{1}{r}\frac{\partial }{\partial \phi }\sum _{n=1}^{N}\sum _{m=2}^{M}{H}_{n}(x)(\text{cos}{\mathrm{m\phi u}}_{\text{nm}}^{i}+\text{sin}{\mathrm{m\phi u}}_{\text{nm}}^{o})\\ +\frac{\zeta }{a}\frac{\partial }{\partial x}\sum _{n=1}^{N}{H}_{n}(x)\left[\text{sin}{\mathrm{\phi w}}_{\mathrm{n1}}^{i}-\text{cos}{\mathrm{\phi w}}_{\mathrm{n1}}^{o}+\sum _{m=2}^{M}(\text{sin}{\mathrm{m\phi v}}_{\text{nm}}^{i}+\text{cos}{\mathrm{m\phi v}}_{\text{nm}}^{o})\right]\\ -(\frac{\zeta }{r}+\frac{\zeta }{r})\frac{{\partial }^{2}}{\partial x\partial \phi }\sum _{n=1}^{N}{H}_{n}(x)\left[{w}_{n}^{o}+\sum _{m=1}^{M}(\text{cos}{\mathrm{m\phi w}}_{\text{nm}}^{i}+\text{sin}{\mathrm{m\phi w}}_{\text{nm}}^{o})\right]\\ {\gamma }_{\mathrm{x\zeta }}=0\end{array}\)

Or again:

\(\begin{array}{}{\varepsilon }_{\text{xx}}=\sum _{n=1}^{N}\sum _{m=2}^{M}{H}_{n}^{\text{'}}(x)(\text{cos}m\phi {u}_{\text{nm}}^{i}+\text{sin}m\phi {u}_{\text{nm}}^{o})\\ -\zeta \sum _{n=1}^{N}{H}_{n}^{\text{'}\text{'}}(x)\left[{w}_{n}^{o}+\sum _{m=1}^{M}(\text{cos}m\phi {w}_{\text{nm}}^{i}+\text{sin}m\phi {w}_{\text{nm}}^{o})\right]\\ {\varepsilon }_{\phi \phi }=\frac{1}{r}\sum _{n=1}^{N}{H}_{n}(x)\left[\text{cos}\phi {w}_{\mathrm{n1}}^{i}+\text{sin}\phi {w}_{\mathrm{n1}}^{o}+\sum _{m=2}^{M}(m\text{cos}m\phi {v}_{\text{nm}}^{i}-m\text{sin}m\phi {v}_{\text{nm}}^{o})\right]\\ +\frac{1}{r}\sum _{n=1}^{N}{H}_{n}(x)\left[{w}_{n}^{o}+\sum _{m=1}^{M}(\text{cos}m\phi {w}_{\text{nm}}^{i}+\text{sin}{\mathrm{mfw}}_{\text{nm}}^{o})\right]\\ +\frac{\zeta }{\mathrm{ar}}\sum _{n=1}^{N}{H}_{n}(x)\left[\text{cos}\phi {w}_{\mathrm{n1}}^{i}+\text{sin}\phi {w}_{\mathrm{n1}}^{o}+\sum _{m=2}^{M}(m\text{cos}m\phi {v}_{\text{nm}}^{i}-m\text{sin}m\phi {v}_{\text{nm}}^{o})\right]\\ +\frac{\zeta }{\mathrm{ar}}\sum _{n=1}^{N}{H}_{n}(x)\left[\sum _{m=1}^{M}({m}^{2}\text{cos}m\phi {w}_{\text{nm}}^{i}+{m}^{2}\text{sin}m\phi {w}_{\text{nm}}^{o})\right]\\ {\gamma }_{x\phi }=\sum _{n=1}^{N}{H}_{n}^{\text{'}}(x)\left[\text{sin}\phi {w}_{\mathrm{n1}}^{i}-\text{cos}{\mathrm{fw}}_{\mathrm{n1}}^{o}\sum _{m=2}^{M}(\text{sin}m\phi {v}_{\text{nm}}^{i}+\text{cos}m\phi {v}_{\text{nm}}^{o})\right]\\ +\frac{1}{r}\sum _{n=1}^{N}\sum _{m=2}^{M}{H}_{n}(x)(-m\text{sin}m\phi {u}_{\text{nm}}^{i}+m\text{cos}m\phi {u}_{\text{nm}}^{o})\\ +\frac{\zeta }{a}\sum _{n=1}^{N}{H}_{n}^{\text{'}}(x)\left[\text{sin}\phi {w}_{\mathrm{n1}}^{i}-\text{cos}\phi {w}_{\mathrm{n1}}^{o}\sum _{m=2}^{M}(\text{sin}m\phi {v}_{\text{nm}}^{i}+\text{cos}m\phi {v}_{\text{nm}}^{o})\right]\\ -(\frac{\zeta }{r}+\frac{\zeta }{a})\sum _{n=1}^{N}{H}_{n}^{\text{'}}(x)\left[\sum _{m=1}^{M}(-m\text{sin}m\phi {w}_{\text{nm}}^{i}+m\text{cos}m\phi {w}_{\text{nm}}^{o})\right]\\ {\gamma }_{x\zeta }=0\end{array}\)

This is given in matrix form:

\((\begin{array}{c}{e}_{\text{xx}}^{s}\\ {e}_{\text{ff}}^{s}\\ {g}_{\mathrm{xf}}^{s}\\ {g}_{\mathrm{xz}}^{s}\end{array})=\sum _{k=1}^{N}{B}_{k}^{s}{U}_{k}^{s}\) with: \({B}_{k}^{s}=(\begin{array}{ccccccc}{B}_{km=2}^{\text{si}}& \cdots & {B}_{km=M}^{\text{si}}& {B}_{km=2}^{\text{so}}& \cdots & {B}_{km=M}^{\text{so}}& {B}_{k}^{\text{sg}}\end{array})\)

where:

\({B}_{\text{km}}^{\text{si}}=(\begin{array}{ccc}{H}_{k}^{\text{'}}\text{cos}(\mathrm{m\phi })& 0& -\zeta {H}_{k}^{\text{'}\text{'}}\text{cos}(\mathrm{m\phi })\\ 0& \frac{m}{r}{H}_{k}\text{cos}(\mathrm{m\phi })(1+\frac{\zeta }{a})& \frac{1}{r}{H}_{k}\text{cos}(\mathrm{m\phi })(1+\frac{\zeta {m}^{2}}{a})\\ -\frac{m}{r}{H}_{k}\text{sin}(\mathrm{m\phi })& {H}_{k}^{\text{'}}\text{sin}(\mathrm{m\phi })(1+\frac{\zeta }{a})& (\frac{\zeta }{r}+\frac{\zeta }{a})m{H}_{k}^{\text{'}}\text{sin}(\mathrm{m\phi })\\ 0& 0& 0\end{array})\),

\({B}_{\text{km}}^{\text{so}}=(\begin{array}{ccc}{H}_{k}^{\text{'}}\text{sin}(\mathrm{m\phi })& 0& -\zeta {H}_{k}^{\text{'}\text{'}}\text{sin}(\mathrm{m\phi })\\ 0& -\frac{m}{r}{H}_{k}\text{sin}(\mathrm{m\phi })(1+\frac{\zeta }{a})& \frac{1}{r}{H}_{k}\text{sin}(\mathrm{m\phi })(1+\frac{\zeta {m}^{2}}{a})\\ \frac{m}{r}{H}_{k}\text{cos}(\mathrm{m\phi })& {H}_{k}^{\text{'}}\text{cos}(\mathrm{m\phi })(1+\frac{\zeta }{a})& -(\frac{\zeta }{r}+\frac{\zeta }{a})m{H}_{k}^{\text{'}}\text{cos}(\mathrm{m\phi })\\ 0& 0& 0\end{array})\)

and

\({B}_{k}^{\text{sg}}=(\begin{array}{ccc}-\zeta {H}_{k}^{\text{'}\text{'}}\text{cos}(\phi )& -\zeta {H}_{k}^{\text{'}\text{'}}\text{sin}(\phi )& -\zeta {H}_{k}^{\text{'}\text{'}}\\ \frac{2}{r}(1+\frac{\zeta }{a}){H}_{k}\text{cos}(\phi )& \frac{2}{r}(1+\frac{\zeta }{a}){H}_{k}\text{sin}(\phi )& \frac{{H}_{k}}{r}\\ (1+\frac{2\zeta }{a}+\frac{\zeta }{r}){H}_{k}^{\text{'}}\text{sin}(\phi )& -(1+\frac{2\zeta }{a}+\frac{\zeta }{r}){H}_{k}^{\text{'}}\text{cos}(\phi )& 0\\ 0& 0& 0\end{array})\)

4.3. Discretization of the total deformation field

\((\begin{array}{c}{\epsilon }_{\text{xx}}\\ {\epsilon }_{\text{φφ}}\\ {\gamma }_{\mathrm{x\phi }}\\ {\gamma }_{\mathrm{x\zeta }}\end{array})=(\begin{array}{c}{\epsilon }_{\text{xx}}^{P}\\ {\epsilon }_{\text{φφ}}^{P}\\ {\gamma }_{\mathrm{x\phi }}^{P}\\ {\gamma }_{\mathrm{x\zeta }}^{P}\end{array})+(\begin{array}{c}{\epsilon }_{\text{xx}}^{s}\\ {\epsilon }_{\text{φφ}}^{s}\\ {\gamma }_{\mathrm{x\phi }}^{s}\\ {\gamma }_{\mathrm{x\zeta }}^{s}\end{array})=\sum _{k=1}^{N}{B}_{k}^{P}{U}_{k}^{P}+\sum _{k=1}^{N}{B}_{k}^{s}{U}_{k}^{s}=\sum _{k=1}^{N}{B}_{k}{U}_{k}=BU\) with

\(B={({B}_{k}^{P}{B}_{k}^{s})}_{k=\mathrm{1,}N}\) and \(U={(\begin{array}{c}{U}_{k}^{P}\\ {U}_{k}^{s}\end{array})}_{k=\mathrm{1,}N}\)

4.4. Stiffness matrix

The variational formulation of deformation work is:

\(\delta {W}_{\text{def}}=\underset{0}{\overset{l}{\int }}\underset{0}{\overset{\mathrm{2\pi }}{\int }}\underset{-h/2}{\overset{h/2}{\int }}\left\{(\begin{array}{cccc}{\text{δε}}_{\text{xx}}& {\text{δε}}_{\text{φφ}}& {\text{δγ}}_{\mathrm{x\phi }}& {\text{δγ}}_{\mathrm{x\zeta }}\end{array})(\begin{array}{c}{\sigma }_{\text{xx}}\\ {\sigma }_{\text{φφ}}\\ {\sigma }_{\mathrm{x\phi }}\\ {\sigma }_{\mathrm{x\zeta }}\end{array})\right\}\text{rd}\phi \text{dxd}\zeta\)

or again:

\(\delta {W}_{\text{def}}=\underset{0}{\overset{l}{\int }}\underset{0}{\overset{\mathrm{2\pi }}{\int }}\underset{-h/2}{\overset{h/2}{\int }}\left\{(\begin{array}{cccc}{\epsilon }_{\text{xx}}& {\epsilon }_{\text{φφ}}& {\gamma }_{\mathrm{x\phi }}& {\gamma }_{\mathrm{x\zeta }}\end{array})C(\begin{array}{c}{\text{δε}}_{\text{xx}}\\ {\text{δε}}_{\text{φφ}}\\ {\text{δγ}}_{\mathrm{x\phi }}\\ {\text{δγ}}_{\mathrm{x\zeta }}\end{array})\right\}\text{rd}\phi \text{dxd}\zeta\)

\(\begin{array}{}{\mathrm{dW}}_{\text{def}}=\underset{0}{\overset{l}{\int }}\underset{0}{\overset{2\pi }{\int }}\underset{-h/2}{\overset{h/2}{\int }}\left\{{(\sum _{k=1}^{N}{B}_{k}{U}_{k})}^{T}C(\sum _{k=1}^{N}{B}_{k}\delta {U}_{k})\right\}rd\phi \mathrm{dx}d\zeta \\ =\underset{0}{\overset{l}{\int }}\underset{0}{\overset{2\pi }{\int }}\underset{-h/2}{\overset{h/2}{\int }}\left\{(\sum _{k=1}^{N}{U}_{{k}^{T}}{B}_{{k}^{T}})C(\sum _{k=1}^{N}{B}_{k}\delta {U}_{k})\right\}rd\phi \mathrm{dx}d\zeta \\ =\underset{0}{\overset{l}{\int }}\underset{0}{\overset{2\pi }{\int }}\underset{-h/2}{\overset{h/2}{\int }}\left\{(\begin{array}{ccc}{U}_{{1}^{T}}& \mathrm{...}& {U}_{{N}^{T}}\end{array}){B}^{T}\mathrm{CB}(\begin{array}{c}\delta {U}_{1}\\ \mathrm{...}\\ \delta {U}_{N}\end{array})\right\}rd\phi \mathrm{dx}d\zeta \\ =(\begin{array}{ccc}{U}_{{1}^{T}}& \mathrm{...}& {U}_{{N}^{T}}\end{array})K(\begin{array}{c}\delta {U}_{1}\\ \mathrm{...}\\ \delta {U}_{N}\end{array})\end{array}\)

The principle of virtual work is then written \({\mathrm{\delta U}}^{T}KU=F\mathrm{\delta U}\) where \(K\) is the stiffness matrix which is equal to:

\(K=\underset{0}{\overset{l}{\int }}\underset{0}{\overset{\mathrm{2\pi }}{\int }}\underset{-h/2}{\overset{h/2}{\int }}\left\{{B}^{T}\text{C B}\right\}\text{r d}\phi \text{dxd}\zeta\)

Note:

We do not make any assumptions about the law of behavior. This expression is therefore in particular valid in the case of non-linear behaviors (plasticity) .

4.5. Mass matrix

The terms of the mass matrix are obtained after discretizing the following variational formulation of the non-centrifugal inertia terms:

\({\mathrm{dW}}_{\text{mass}}^{\text{ac}}=\underset{0}{\overset{l}{\int }}\underset{0}{\overset{\mathrm{2p}}{\int }}\underset{-h/2}{\overset{+h/2}{\int }}\rho \ddot{u}\text{.}\mathrm{dv}\text{rdxd}\mathrm{fdz}\) with \(u=(\begin{array}{c}{u}_{1}(x,\phi ,r)\\ {u}_{2}(x,\phi ,r)\\ {u}_{3}(x,\phi ,r)\\ u(x,\phi ,r)\\ v(x,\phi ,r)\\ w(x,\phi ,r)\end{array})\).

The notations used are those of [§2.1]: \({u}_{1},{u}_{2}\) and \({u}_{3}\) are the movements of the beam at a point in the section and \(u,v\) and \(w\) are the movements of the average fiber of this section at this same point.

Discretization then gives:

\(u=\sum _{k=1}^{N}{H}_{k}{N}_{k}(\begin{array}{c}{u}_{x}^{k}\\ {u}_{y}^{k}\\ {u}_{z}^{k}\\ {\theta }_{x}^{k}\\ {\theta }_{y}^{k}\\ {\theta }_{z}^{k}\\ {u}_{\text{km}}^{i}\\ {v}_{\text{km}}^{i}\\ {w}_{\text{km}}^{i}\\ {u}_{\text{km}}^{o}\\ {v}_{\text{km}}^{o}\\ {w}_{\text{km}}^{o}\\ {w}_{\mathrm{k1}}^{i}\\ {w}_{\mathrm{k1}}^{o}\\ {w}_{k}^{o}\end{array})\) \(\begin{array}{}\\ \\ \\ \\ \\ \\ \end{array}\}m=\mathrm{2,}M\)

where the expression for \({N}_{k}\) matrices is:

\({N}_{k}=\left[\begin{array}{ccccccccccccccc}{x}_{k}\cdot x& {y}_{k}\cdot x& 0& -r\mathrm{cos}\phi ({x}_{k}\cdot y)& -r\mathrm{cos}\phi ({y}_{k}\cdot y)& r\mathrm{sin}\phi & 0& & & \text{...}& & & 0& 0& 0\\ {x}_{k}\cdot y& {y}_{k}\cdot y& 0& r\mathrm{cos}\phi ({x}_{k}\cdot x)& r\mathrm{cos}\phi ({y}_{k}\cdot x)& 0& 0& & & \text{...}& & & 0& 0& 0\\ 0& 0& 1& -r\mathrm{sin}\phi ({x}_{k}\cdot x)& -r\mathrm{sin}\phi ({y}_{k}\cdot y)& 0& 0& & & \text{...}& & & 0& 0& 0\\ 0& & & \text{...}& & & \mathrm{cos}(m\phi )& 0& 0& \mathrm{sin}(m\phi )& 0& 0& 0& 0& 0\\ 0& & & \text{...}& & & 0& \mathrm{sin}(m\phi )& 0& 0& \mathrm{cos}(m\phi )& 0& \mathrm{sin}(\phi )& \mathrm{cos}(\phi )& 0\\ 0& & & \text{...}& & & 0& 0& \mathrm{cos}(m\phi )& 0& 0& \mathrm{sin}(m\phi )& \mathrm{cos}(\phi )& \mathrm{sin}(\phi )& 1\end{array}\right]\)

The mass matrix then has the following expression:

\(M=\underset{0}{\overset{l}{\int }}\underset{0}{\overset{\mathrm{2\pi }}{\int }}\underset{-h/2}{\overset{+h/2}{\int }}\rho {N}^{T}N\text{rdxd}\mathrm{\phi d\zeta }\).

with

\(N={({H}_{k}{N}_{k})}_{k=\mathrm{1,}N}\).

Note:

In the case of the straight pipe, we have \({x}_{k}\text{.}x={y}_{k}\text{.}y=1\) and \({x}_{k}\text{.}y={y}_{k}\text{.}x=0\) .

4.6. Shape functions

Functions of at least quadratic shape are chosen for the beam part (displacements and rotations) in order to avoid numerical blocking phenomena [bib3]. This choice involves the use of a finite element with three or four nodes. In the case of an element with 3 nodes, the shape functions are quadratic, and for an element with 4 nodes, the shape functions will be cubic. For the additional part, we choose to take the same shape functions as for the beam part.

The quadratic form functions (element with 3 nodes) are as follows:

\(\begin{array}{}{H}_{1}(x)=(\frac{\mathrm{2x}}{l}-1)(\frac{x}{l}-1)\\ {H}_{2}(x)=\frac{x}{l}(\frac{\mathrm{2x}}{l}-1)\\ {H}_{3}(x)=-4\frac{x}{l}(\frac{x}{l}-1)\end{array}\)

The cubic form functions (element with 4 nodes) are the Lagrange functions of order 3:

\(\begin{array}{c}{H}_{1}(x)\mathrm{=}\frac{(\xi \mathrm{-}{\xi }_{2})(\xi \mathrm{-}{\xi }_{3})(\xi \mathrm{-}{\xi }_{4})}{({\xi }_{1}\mathrm{-}{\xi }_{2})({\xi }_{1}\mathrm{-}{\xi }_{3})({\xi }_{1}\mathrm{-}{\xi }_{4})}\\ {H}_{2}(x)\mathrm{=}\frac{(\xi \mathrm{-}{\xi }_{1})(\xi \mathrm{-}{\xi }_{3})(\xi \mathrm{-}{\xi }_{4})}{({\xi }_{2}\mathrm{-}{\xi }_{1})({\xi }_{2}\mathrm{-}{\xi }_{3})({\xi }_{2}\mathrm{-}{\xi }_{4})}\\ {H}_{3}(x)\mathrm{=}\frac{(\xi \mathrm{-}{\xi }_{1})(\xi \mathrm{-}{\xi }_{2})(\xi \mathrm{-}{\xi }_{4})}{({\xi }_{3}\mathrm{-}{\xi }_{1})({\xi }_{3}\mathrm{-}{\xi }_{2})({\xi }_{3}\mathrm{-}{\xi }_{4})}\\ {H}_{4}(x)\mathrm{=}\frac{(\xi \mathrm{-}{\xi }_{1})(\xi \mathrm{-}{\xi }_{2})(\xi \mathrm{-}{\xi }_{3})}{({\xi }_{4}\mathrm{-}{\xi }_{1})({\xi }_{4}\mathrm{-}{\xi }_{2})({\xi }_{4}\mathrm{-}{\xi }_{3})}\\ \mathrm{-}1\mathrm{\le }\xi \mathrm{\le }1\end{array}\)

4.7. Digital integration

The integration is done by the Gauss method along the middle fiber, the Simpson method in the thickness and on the circumference. For Gauss integration, 3 integration points are used for elements with 3 nodes, as for elements with 4 nodes (these are therefore under-integrated). Integration into the thickness is an integration by layers, the number of which can be fixed later by the user. For each layer we take 3 Simpson points, the 2 end points being common with the neighboring layers. So for \(n\) layers we use \(\mathrm{2n}+1\) points. The number of sectors for integration on the circumference can also be set later by the user. Currently the numbers of layers and sectors are set to their maximum value: 3 layers (7 points) and 16 sectors (33 points), which gives a total of 693 integration points. Simpson integration is equivalent to calculating the sum of the values of the function at the integration points (the ends and the middle of each layer or sector) affected by the weights given by the table below.

Point coordinates	Weight
\(-\sqrt{(3/5)}\) = -0.77459666969241483	5/9=0.55555555555555555555556
0	8/9=0.888888888888888888889
\(\sqrt{(3/5)}\) =0.774596669241483	5/9=0.55555555555555555555556

Gauss integration on medium fiber

\(\frac{1}{3}\frac{4}{3}\frac{2}{3}\frac{4}{3}\frac{2}{3}\mathrm{.....}\frac{2}{3}\frac{4}{3}\frac{2}{3}\frac{4}{3}\frac{1}{3}\)

Weight of integration points for the Simpson method

So for a function \(f(x,\phi ,\zeta )\) on a straight geometry we have:

\(\begin{array}{}\underset{0}{\overset{l}{\int }}\underset{0}{\overset{2\pi }{\int }}\underset{-h/2}{\overset{h/2}{\int }}f(x,\phi ,\zeta )r\text{dx}\mathrm{d\phi }\mathrm{d\zeta }=\frac{l}{2}\underset{-1}{\overset{1}{\int }}\underset{0}{\overset{2\pi }{\int }}\underset{-h/2}{\overset{h/2}{\int }}\tilde{f}(\tilde{x},\phi ,\zeta )rd\tilde{x}\mathrm{d\phi }\mathrm{d\zeta }\\ =\frac{l}{2}\frac{h}{2{N}_{\text{COU}}}\frac{\mathrm{2\pi }}{2{N}_{\text{SECT}}}\sum _{k=1}^{\text{NPG}}\sum _{n=1}^{{\mathrm{2N}}_{\text{COU}}+1}\sum _{m=1}^{{\mathrm{2N}}_{\text{SECT}}+1}\left[{w}_{k}{w}_{n}{w}_{m}{r}_{{N}_{\text{COU}}}\tilde{f}({\tilde{x}}_{\text{NPG}},{\phi }_{{N}_{\text{SECT}}},{\zeta }_{{N}_{\text{COU}}})\right]\end{array}\)

the \({w}_{k}{w}_{n}{w}_{m}\) being respectively the integration weights over the length, on the circumference and in the thickness, ordered as shown in the two tables above.

4.8. Discretization of external work

The variational formulation of the external energy for the beam part is written as: \(\begin{array}{}{\mathrm{\delta W}}_{\text{ext}}^{p}=\underset{0}{\overset{l}{\int }}({f}_{x}{\mathrm{\delta u}}_{x}+{f}_{y}{\mathrm{\delta u}}_{y}+{f}_{z}{\mathrm{\delta u}}_{z}+{m}_{x}{\text{δθ}}_{x}+{m}_{y}{\text{δθ}}_{y}+{m}_{z}{\text{δθ}}_{z})\text{dx}+\\ [{\phi }_{x}{\mathrm{\delta u}}_{x}+{\phi }_{y}{\mathrm{\delta u}}_{y}+{\phi }_{z}{\mathrm{\delta u}}_{z}+{\mu }_{x}{\text{δθ}}_{x}+{\mu }_{y}{\text{δθ}}_{y}+{\mu }_{z}{\text{δθ}}_{z}{]}_{\mathrm{0,}l}\end{array}\)

and for the additional part it is written taking into account only the pressure load: \({\mathrm{\delta W}}_{\text{ext}}^{s}=\underset{0}{\overset{l}{\int }}{F}_{r}\mathrm{\delta w}\text{dx}+[{\Phi }_{r}\mathrm{\delta w}{]}_{\mathrm{0,}l}\)

Taking into account the discretization of travel, we can write:

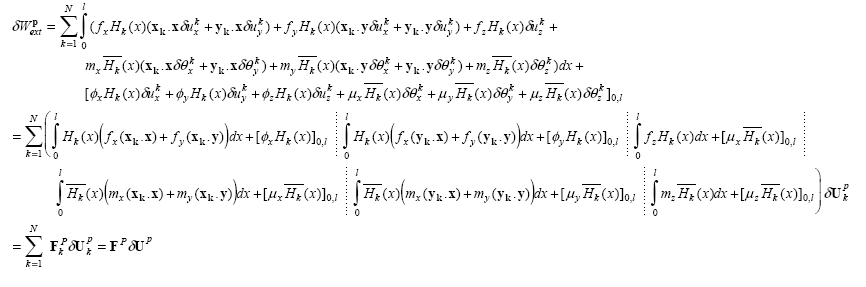
and

\(\begin{array}{}\delta {W}_{\text{ext}}^{s}=\sum _{k=1}^{N}(\underset{0}{\overset{l}{\int }}{F}_{r}{H}_{k}(x){\mathrm{dw}}_{k}^{o}\text{dx}+[{F}_{r}{H}_{k}(x){\mathrm{dw}}_{k}^{o}{]}_{\mathrm{0,}l})\\ =\sum _{k=1}^{N}(\begin{array}{ccccccc}0& 0& 0& 0& 0& 0& \underset{0}{\overset{l}{\int }}{F}_{r}{H}_{k}(x)\text{dx}+[{F}_{r}{H}_{k}(x){]}_{\mathrm{0,}l}\end{array})\delta {U}_{k}^{s}\\ =\sum _{k=1}^{N}{F}_{k}^{s}\delta {U}_{k}^{s}={F}^{s}\delta {U}^{s}\end{array}\)

Note:

For extreme elbow knots we have \({x}_{k}\text{.}x={y}_{k}\text{.}y=1\) and \({x}_{k}\text{.}y={y}_{k}\text{.}x=0\). In the case of the straight pipe, we have \({x}_{k}\text{.}x={y}_{k}\text{.}y=1\) and \({x}_{k}\text{.}y={y}_{k}\text{.}x=0\) for the whole element.