10. Description of document versions#
Version Aster |
Author (s) Organization (s) |
Description of changes |
5 |
P.Massin, A.Laulusa EDF -R&D/ MMN |
Initial text |
7.4 |
X.Desroches |
Update: minor changes |
Unprogrammed extension to anisotropic materials
It is considered that the shell consists of an orthotropic material, orthotropic axes \({\tilde{\tilde{x}}}_{k}\) associated with the base \({k}_{k}\). The law of behavior in these axes is written as:
\(\underset{(6\mathrm{\times }1)}{\tilde{\tilde{\varepsilon }}}\mathrm{=}\underset{(6\mathrm{\times }6)}{{\tilde{\tilde{S}}}_{k}}\underset{(6\mathrm{\times }1)}{\tilde{\tilde{\sigma }}}\)
where \(\tilde{S}\) is the flexibility matrix of the component \(k\).
Let \(\tilde{\varepsilon }\) and \(\tilde{\sigma }\) be the deformation and stress tensors in the \({\tilde{x}}_{k}\) axes, we have:
\(\begin{array}{c}\tilde{\sigma }\mathrm{=}{}^{t}\text{}Q\tilde{\tilde{\sigma }}Q\\ \tilde{\varepsilon }\mathrm{=}{}^{t}\text{}Q\tilde{\tilde{\varepsilon }}Q\end{array}\)
where \(Q\mathrm{=}{\left[{T}_{1},{T}_{2},{T}_{3}\right]}_{\mathrm{/}{k}_{k}}\) (\({Q}_{\text{ij}}={T}_{i}\text{.}{k}_{j}\)) is the direction cosine matrix of \({T}_{k}\) in base \({k}_{k}\).
In vector form, we have:
\(\begin{array}{c}\tilde{\sigma }\mathrm{=}\tilde{T}\tilde{\tilde{\sigma }}\\ \tilde{\varepsilon }\mathrm{=}\tilde{T}\tilde{\tilde{\varepsilon }}\end{array}\)
where the components of \(\tilde{T}\) are defined according to those of \(Q\).
Conversely, we have:
\(\begin{array}{c}\tilde{\tilde{\sigma }}\mathrm{=}{\tilde{T}}^{\text{-1}}\tilde{\sigma }\\ \tilde{\tilde{\varepsilon }}\mathrm{=}{\tilde{T}}^{\text{-1}}\tilde{\varepsilon }\end{array}\)
so, we get:
\(\tilde{\varepsilon }\mathrm{=}\tilde{T}{\tilde{\tilde{S}}}_{k}{\tilde{T}}^{\mathrm{-}1}\tilde{\sigma }\)
that we write:
\(\tilde{\varepsilon }\mathrm{=}{\tilde{S}}_{k}\tilde{\sigma }\)
To be consistent with the plane stress hypothesis \({\tilde{\sigma }}_{\text{33}}\mathrm{=}0\), we write:
\(\underset{(5\mathrm{\times }1)}{{\tilde{\varepsilon }}_{r}}\mathrm{=}\underset{(5\mathrm{\times }5)}{{\tilde{S}}_{\text{kr}}}\underset{(5\mathrm{\times }1)}{{\tilde{\sigma }}_{r}}\)
with the symbol r as a reduced one, which gives:
\({\tilde{\sigma }}_{r}\mathrm{=}{\tilde{C}}_{k}{\tilde{\varepsilon }}_{r},{\tilde{C}}_{k}\mathrm{=}{\tilde{S}}_{\text{kr}}^{\mathrm{-}1}\)
that we rewrite by omitting the symbol \(r\),
\(\tilde{\sigma }\mathrm{=}{\tilde{C}}_{k}\tilde{\varepsilon }\)
The elastic deformation energy \({W}^{\text{el}}\) is:
\({W}^{\text{el}}\mathrm{=}\frac{1}{2}{}^{t}\text{}{\tilde{q}}^{e}\underset{\mathrm{-}1}{\overset{1}{\mathrm{\int }}}\underset{\text{Ar}}{\overset{}{\mathrm{\int }}}{}^{t}\text{}\tilde{B}{\tilde{C}}_{k}\tilde{B}\text{det}Jd{\xi }_{1}d{\xi }_{2}d{\xi }_{3}{\tilde{q}}^{e}\)
If the shell consists of \(\mathit{Nc}\) layers, with each layer considered to be a \(k\) component, then:
\({W}^{\text{el}}\mathrm{=}\frac{1}{2}{}^{t}\text{}{\tilde{q}}^{e}\mathrm{\sum }_{k\mathrm{=}1}^{\text{Nc}}\underset{2{e}_{k}^{\mathrm{-}}\mathrm{/}h}{\overset{2{e}_{k}^{+}\mathrm{/}h}{\mathrm{\int }}}\underset{\text{Ar}}{\overset{}{\mathrm{\int }}}{}^{t}\text{}\tilde{B}\tilde{{C}_{k}}\stackrel{}{˜}B\text{det}Jd{\xi }_{1}d{\xi }_{2}d{\xi }_{3}{\stackrel{}{˜}q}^{e}\)
where \({e}_{k}^{\mathrm{-}}\) and \({e}_{k}^{+}\) are the abscissa of the lower and upper terminals of the \(k\) thick layer
\({e}_{k}\mathrm{=}{e}_{k}^{+}\mathrm{-}{e}_{k}^{\mathrm{-}}\), with \({e}_{1}^{\mathrm{-}}\mathrm{=}\mathrm{-}h\mathrm{/}2\) and \({e}_{\text{Nc}}^{+}\mathrm{=}h\mathrm{/}2\).
By posing:
\({\xi }_{3}\mathrm{=}\frac{{e}_{k}}{h}{\overline{\xi }}_{3}+\frac{{e}_{k}^{+}+{e}_{k}^{\mathrm{-}}}{h},{\overline{\xi }}_{3}\mathrm{\in }\left[\mathrm{-}\mathrm{1,1}\right]\)
we have:
\({W}^{\text{el}}\mathrm{=}\frac{1}{2}{}^{t}\text{}{\tilde{q}}^{e}\mathrm{\sum }_{k\mathrm{=}1}^{\text{Nc}}\frac{{e}_{k}}{h}\underset{\mathrm{-}1}{\overset{1}{\mathrm{\int }}}\underset{\text{Ar}}{\overset{}{\mathrm{\int }}}{}^{t}\text{}\tilde{B}{\tilde{C}}_{k}\tilde{B}\text{det}J({\xi }_{1},{\xi }_{2},{\overline{\xi }}_{3})d{\xi }_{1}d{\xi }_{2}d{\overline{\xi }}_{3}{\tilde{q}}^{e}\)
Likewise, for the work due to thermal expansion \({W}^{\text{th}}\), we have:
\({\tilde{\tilde{\varepsilon }}}_{\text{th}}^{k}\mathrm{=}({\alpha }_{1}^{k}T,{\alpha }_{2}^{k}T,{\alpha }_{3}^{k}T\mathrm{,0}\mathrm{,0}\mathrm{,0})\)
where \({\alpha }_{i}^{k}\) are the thermal expansion coefficients of layer \(k\) in the orthotropic axes (\({\tilde{\tilde{\xi }}}_{k}\)).
With the relationship:
\({\tilde{\varepsilon }}_{\text{th}}^{k}\mathrm{=}\tilde{T}{\tilde{\tilde{\varepsilon }}}_{\text{th}}^{k}\)
we get:
\({W}^{\text{th}}\text{=-}{}^{t}\text{}{\tilde{q}}^{e}\underset{\mathrm{-}1}{\overset{1}{\mathrm{\int }}}\underset{\text{Ar}}{\overset{}{\mathrm{\int }}}{}^{t}\text{}\tilde{B}(\mathrm{-}{\tilde{C}}_{k}{\tilde{\varepsilon }}_{\text{th}}^{k})\text{det}Jd{\xi }_{1}d{\xi }_{2}d{\xi }_{3}\)
Either:
\({W}^{\text{th}}\mathrm{=}{}^{t}\text{}{\tilde{q}}^{e}\mathrm{\sum }_{h\mathrm{=}1}^{\text{Nc}}\frac{{e}_{k}}{h}\underset{\mathrm{-}1}{\overset{1}{\mathrm{\int }}}\underset{\text{Ar}}{\overset{}{\mathrm{\int }}}{}^{t}\text{}\tilde{B}{\tilde{C}}_{k}{\tilde{\varepsilon }}_{\text{th}}^{k}\text{det}Jd{\xi }_{1}d{\xi }_{2}d{\overline{\xi }}_{3}\)
Shape functions for the Q9H element
These functions are given on page 174 of [bib8].
A2.1 Shape functions for translations
The 8 incomplete Lagrange shape functions of the quadrangle element Q9H [Figure A2.2-a] for the interpolation of the \({u}_{k}\) displacements are:
\({N}_{i}^{(1)}({\xi }_{1},{\xi }_{2})\mathrm{=}\frac{1}{4}(\mathrm{-}1+{\xi }_{\mathrm{1i}}{\xi }_{1}+{\xi }_{\mathrm{2i}}{x}_{2})(1+{\xi }_{\mathrm{1i}}{\xi }_{1})(1+{x}_{\mathrm{2i}}{\xi }_{2})i\mathrm{=}\mathrm{1,2}\mathrm{,3}\mathrm{,4}\)
\({N}_{i}^{(1)}({\xi }_{1},{\xi }_{2})\mathrm{=}\frac{1}{2}(1\mathrm{-}{x}_{1}^{2})(1+{\xi }_{\mathrm{2i}}{\xi }_{2})i\mathrm{=}\mathrm{5,7}\)
\({N}_{i}^{(1)}({\xi }_{1},{\xi }_{2})\mathrm{=}\frac{1}{2}(1\mathrm{-}{x}_{2}^{2})(1+{\xi }_{\mathrm{1i}}{\xi }_{1})i\mathrm{=}\mathrm{6,8}\)
with: \(\begin{array}{c}{\xi }_{\mathrm{1i}}\text{=-}\mathrm{1i}\mathrm{=}\mathrm{1,8}\mathrm{,4};\\ {\xi }_{\mathrm{1i}}\mathrm{=}\mathrm{0i}\mathrm{=}\mathrm{5,7};\\ {\xi }_{\mathrm{1i}}\text{=+}\mathrm{1i}\mathrm{=}\mathrm{2,6}\mathrm{,3}\text{.}\end{array}\) and \(\begin{array}{c}{\xi }_{\mathrm{2i}}\text{=-}\mathrm{1i}\mathrm{=}\mathrm{1,5}\mathrm{,2};\\ {\xi }_{\mathrm{2i}}\mathrm{=}\mathrm{0i}\mathrm{=}\mathrm{6,8};\\ {\xi }_{\mathrm{2i}}\text{=+}\mathrm{1i}\mathrm{=}\mathrm{3,7}\mathrm{,4}\text{.}\end{array}\).
A2.2 Shape functions for rotations
The 9 Lagrange shape functions of the quadrangle element Q9H [Figure A2.2-a] for the interpolation of the \({\tilde{\theta }}_{\alpha }\) rotations are:
\({N}_{i}^{(2)}({x}_{1},{\xi }_{2})\mathrm{=}{N}_{i}({\xi }_{1}){N}_{i}({\xi }_{2})\) where \({N}_{i}({\xi }_{P})\mathrm{=}\underset{\mathit{r¹i}}{P}\frac{{\xi }_{\text{Pr}}\mathrm{-}{\xi }_{P}}{{\xi }_{\text{Pr}}\mathrm{-}{\xi }_{\text{Pi}}}\) for \(p\mathrm{=}\mathrm{1,2}\) and where \(r\) describes the set of two nodes aligned with node \(i\) in the \({\xi }_{P}\) direction.
We have: \(\begin{array}{c}{x}_{\mathrm{1i}}\text{=-}\mathrm{1i}\mathrm{=}\mathrm{1,8}\mathrm{,4};\\ {x}_{\mathrm{1i}}\mathrm{=}\mathrm{0i}\mathrm{=}\mathrm{5,7};\\ {x}_{\mathrm{1i}}\text{=+}\mathrm{1i}\mathrm{=}\mathrm{2,6}\mathrm{,3}\text{.}\end{array}\) and \(\begin{array}{c}{x}_{\mathrm{2i}}\text{=-}\mathrm{1i}\mathrm{=}\mathrm{1,5}\mathrm{,2};\\ {x}_{\mathrm{2i}}\mathrm{=}\mathrm{0i}\mathrm{=}\mathrm{6,8};\\ {x}_{\mathrm{2i}}\text{=+}\mathrm{1i}\mathrm{=}\mathrm{3,7}\mathrm{,4}\text{.}\end{array}\).
Figure A2.2-a: Degrees of freedom for translations and rotations of the quadrangle element Q9H
Shape functions for the T7H element
A3.1 Shape functions for translations
The 6 shape functions of the triangular element T7H [Figure A3.2-a] for interpolating \({u}_{k}\) displacements are given on page 175 of [bib8]:
\({N}_{1}^{(1)}\left({x}_{1},{x}_{2}\right)=\lambda (2\lambda -1)\)
\({N}_{2}^{(1)}\left({x}_{1},{x}_{2}\right)={x}_{1}({\mathrm{2x}}_{1}-1)\)
\({N}_{3}^{(1)}\left({x}_{1},{x}_{2}\right)={x}_{2}({\mathrm{2x}}_{2}-1)\)
\({N}_{4}^{(1)}\left({x}_{1},{x}_{2}\right)={\mathrm{4x}}_{1}\lambda\)
\({N}_{5}^{(1)}\left({x}_{1},{x}_{2}\right)={\mathrm{4x}}_{1}{x}_{2}\)
\({N}_{6}^{(1)}\left({x}_{1},{x}_{2}\right)=4\lambda {x}_{2}\)
where: \(\lambda \mathrm{=}1\mathrm{-}{x}_{1}\mathrm{-}{x}_{2}\)
A3.2 Shape functions for rotations
The 7 shape functions of the triangular element T7H [Figure A3.2-a] for the interpolation of the \({\tilde{q}}_{\alpha }\) rotations are:
\({N}_{1}^{(2)}\left({x}_{1},{x}_{2}\right)=\left(1-{x}_{1}-{x}_{2}\right)\left[2\left(1-{x}_{1}-{x}_{2}\right)-1\right]+\frac{1}{9}{N}_{7}^{(2)}\)
\({N}_{2}^{(2)}\left({x}_{1},{x}_{2}\right)={x}_{1}\left({\mathrm{2x}}_{1}-1\right)+\frac{1}{9}{N}_{7}^{(2)}\)
\({N}_{3}^{(2)}\left({x}_{1},{x}_{2}\right)={x}_{2}\left({\mathrm{2x}}_{2}-1\right)+\frac{1}{9}{N}_{7}^{(2)}\)
\({N}_{4}^{(2)}\left({x}_{1},{x}_{2}\right)={\mathrm{4x}}_{1}\left(1-{x}_{1}-{x}_{2}\right)-\frac{4}{9}{N}_{7}^{(2)}\)
\({N}_{5}^{(2)}\left({x}_{1},{x}_{2}\right)={\mathrm{4x}}_{1}{x}_{2}-\frac{4}{9}{N}_{7}^{(2)}\)
\({N}_{6}^{(2)}\left({x}_{1},{x}_{2}\right)={\mathrm{4x}}_{2}\left(1-{x}_{1}-{x}_{2}\right)-\frac{4}{9}{N}_{7}^{(2)}\)
with:
\({N}_{7}^{(2)}({x}_{1},{x}_{2})\mathrm{=}\text{27}{x}_{1}{x}_{2}(1\mathrm{-}{x}_{1}\mathrm{-}{x}_{2})\)
Figure A3.2-a: Degrees of freedom for translations and rotations of the triangle element T7H
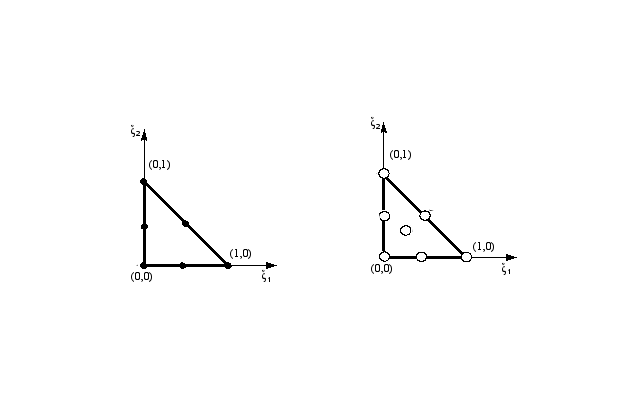
7
6
3
5
2
4
1
6
5
4
3
2
1
6
4
3
1
5
2