2. Model problem

We consider a 2D static elasticity problem, distributed over two processors.

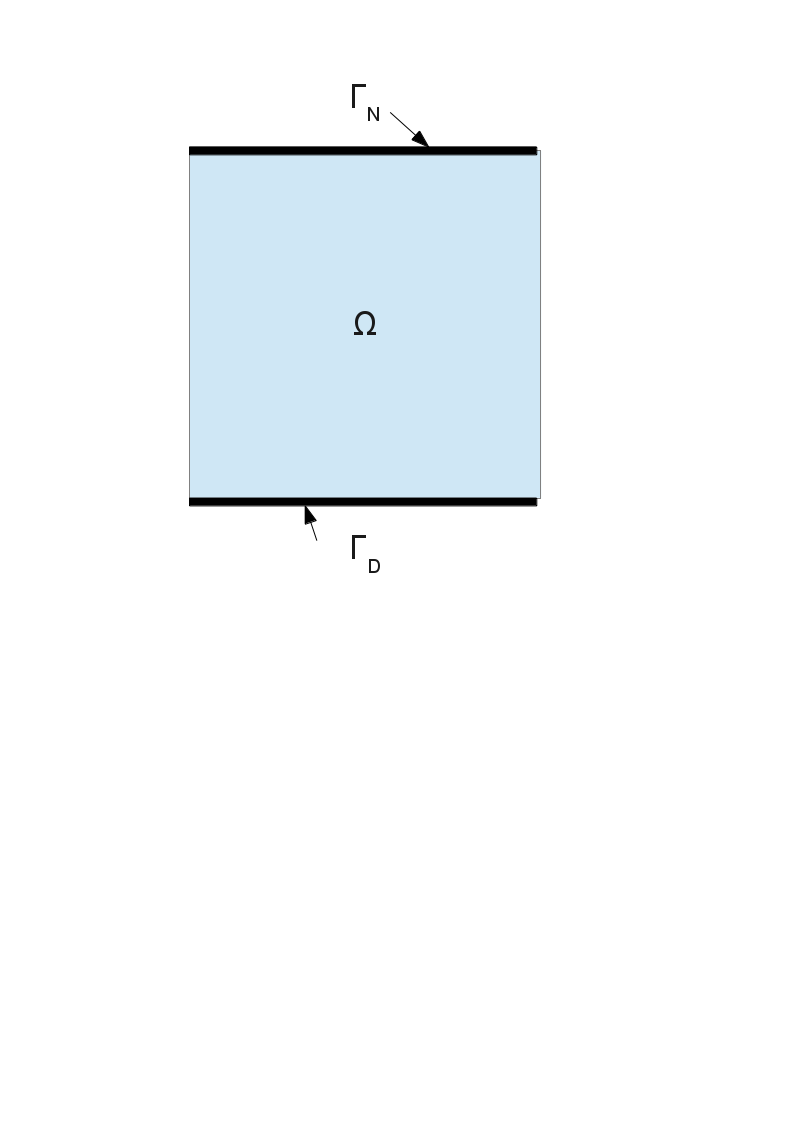
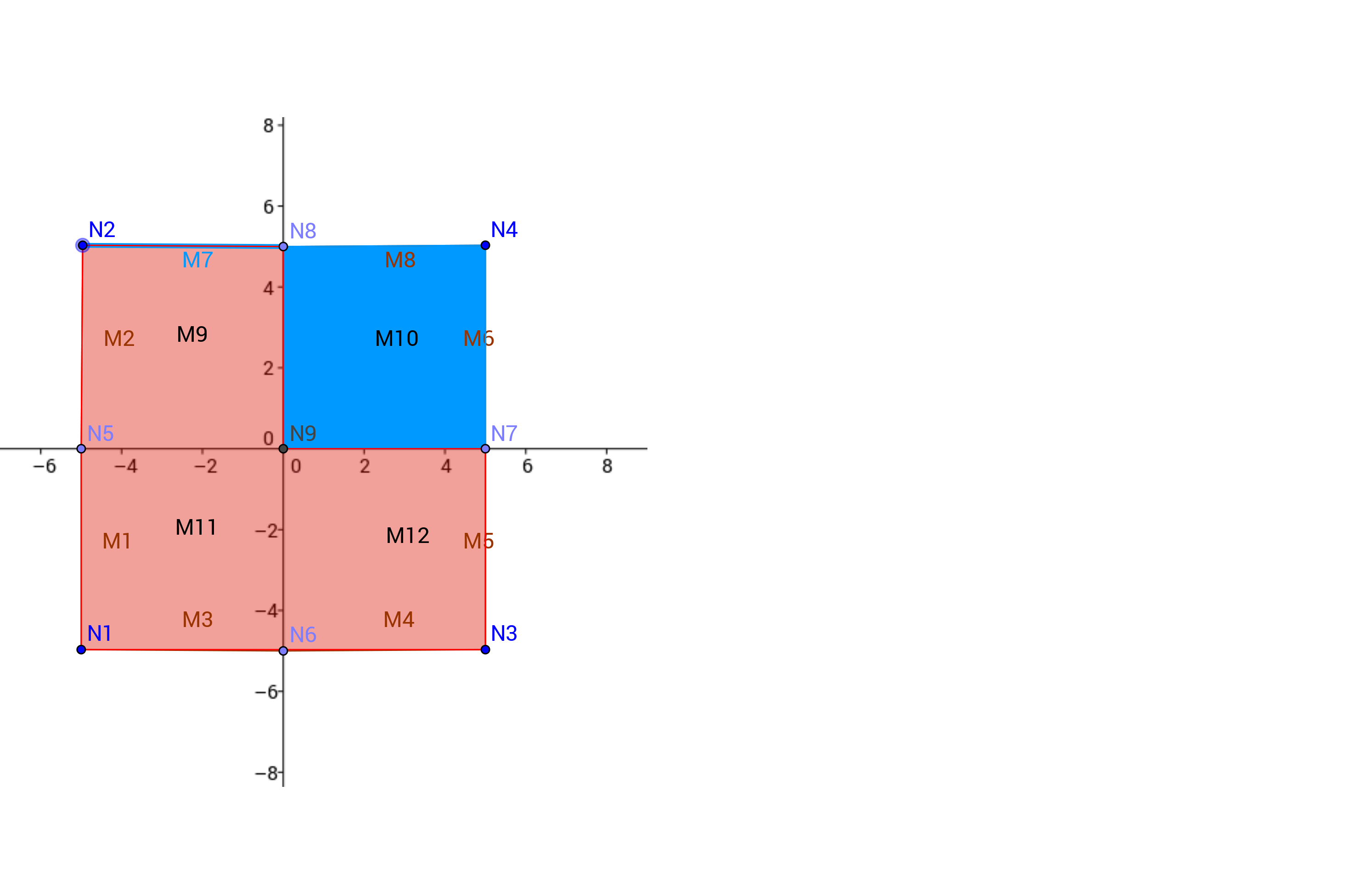
2.1. Geometry

The elastic domain is a square of extreme points (-50.50) and (50.50). We mesh this domain into 4 quadrangles.

Geometry: a uniform pressure is imposed on the GN border and an embedment condition is imposed on the GD border	Meshing: the names of the vertices (N1 to N9) and the meshes (M1 to M12) are in accordance with Code_Aster. There are 8 1D meshes and 4 2D meshes. The blue cells M7, M8 and M10 are assigned to the processor 0. The red meshes M9, M11, and M12 are assigned to the processor 1

2.2. Material properties

• \(E\mathrm{=}\mathrm{1,0}{10}^{11}N\mathrm{/}{m}^{2}\)

• \(\nu \mathrm{=}\mathrm{0,3}\)

2.3. 2D modeling

The model is assigned to the 4 quadrangular cells (group of 2D all cells) and to the 2 segments that constitute the upper edge of the domain (group of elements 1D up).

MODEL = AFFE_MODELE (MAILLAGE =MA,

AFFE =_F (GROUP_MA =( 'all', 'up',),

PHENOMENE =' MECANIQUE ',

MODELISATION ='C_ PLAN ',),

PARALLELISME =_F (DISTRIBUTION =' SOUS_DOMAINE ',),

);

A type of distribution of cells has also been defined (by sub-domain).

2.4. Limit conditions and loading

Pressure is exerted distributed on the upper edge of the square, with ends (-50.50) (50.50):

PRESSION = AFFE_CHAR_MECA (MODELE = MODEL,

PRES_REP =_F (GROUP_MA ='up',

PRES =1000000000,),);

The base of the square is embedded: we apply the condition*DX* =0, DY =0 to the end segment \((-\mathrm{50,}-50)\) \((\mathrm{50,}-50)\).

This embedment is applied in two ways:

• modeling A: with AFFE_CHAR_CINE

  ENCASTR = AFFE_CHAR_CINE (MODELE = MODEL,
  
  MECA_IMPO =_F (GROUP_NO ='bottom',
  
  DX=0,
  
  DY=0,),);
  

• B modeling: with AFFE_CHAR_MECA

  ENCASTR = AFFE_CHAR_MECA (MODELE = MODEL,
  
  DDL_IMPO =_F (GROUP_NO ='bottom',
  
  DX=0,
  
  DY=0,),);
  

2.5. Distribution of the problem

When creating the model, a distribution of the elementary calculations by sub-domain was chosen. We specify to the solver that the matrix is distributed:

MECA_STATIQUE (MODELE = MODEL,

CHAM_MATER = AFMAT,

EXCIT =( _F (CHARGE = PRESSION,),

_F (CHARGE = ENCASTR,),),

SOLVEUR =_F (METHODE =” PETSC “,

MATR_DISTRIBUEE =” OUI “,

ALGORITHME =” GMRES “,),);

The calculation is run on 2 processors.