6. Object STOCKAGE#

Code_Aster’s sparse matrices all have a symmetric structure: if a (i, j) exists, then a (j, i) also exists.

For a sparse symmetric matrix, only its « upper » part (a (i, j) for j≥i) is stored. Data structure STOCKAGE describes how non-zero terms in the upper part of the matrix are stored.

For a non-symmetric matrix, the upper part and the lower part are stored. As these 2 parts have the same structure (except for one transposition), storing the upper part is sufficient.

Note:

Although theoretically, the non-zero terms in a matrix can be arranged in any way, the filling of Code_Aster matrices is such that all the DDLs carried by a node are connected to all the DDLs carried by the other nodes adjacent to this node via a finite element. The matrix is therefore formed of small solid rectangles corresponding to the connectivity of the model nodes. In particular, there are small blocks along the entire diagonal of the matrix.

6.1. Object STOC_LIGN_CIEL#

For the online storage of Ciel, the objects are as follows:

STOC_LCIEL (K19): :=record

♦. SCBL OJB S V I ♦. SCDI OJB S V I ♦. SCDE OJB S V I ♦. SCHC OJB S V I ♦. SCIB OJB S V I ◊ .M2LC OJB S V I ◊. LC2M OJB S V I

. SCDE	S V I dim=4
		number of equations neq size of the blocks of the matrix t_block number of blocks required to store the values of the matrix n_block maximum height of the columns of the matrix
. SCHC	S V I dim=neq
		Height of the 6th column
. SCDI	S V I dim=neq
		Address of the diagonal term of the th-column in its block
. SCBL	S V I dim=n_bloc+1
	(K+1)	0number of the last column in block K note: a column can only belong to one block
. SCIB	S V I dim=neq
		Number of the block that contains the th column of the matrix
.M2LC	S V I dim=neq
	IEQ_M	ieq_lc: gives the correspondence between the numbering of the « Morse » storage (ieq_m) and the numbering of the « sky line » storage (ieq_lc)
. LC2M	S V I dim=neq
	ieq_lc	ieq_m: gives the correspondence between the numbering of the « sky line » storage (ieq_lc) and the numbering of the « Morse » storage (ieq_m)

Example:

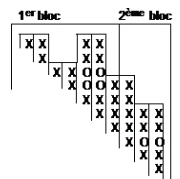
SCDI (1) = 1 SCDI (6) = 17

SCDI (2) = 3 SCDI (7) = 22

SCDI (3) = 4 SCDI (8) = 6

SCDI (4) = 6 SCDI (9) = 11

SCDI (5) = 11 SCDI (10) = 17

SCHC (1) = 1 SCHC (6) = 6

SCHC (2) = 2 SCHC (7) = 5

SCHC (3) = 1 SCHC (8) = 6

SCHC (4) = 2 SCHC (9) = 5

SCHC (5) = 5 SCHC (10) = 6

SCBL (1) = 0 SCIB (1 to 7) = 1

SCBL (2) = 7 SCIB (7 to 10) = 2

SCBL (3) = 10

6.2. Object STOC_MORSE#

For morse storage, the objects are as follows:

STOC_MORSE (K19): :=record

♦. SMDI OJB S V I ♦. SMDE OJB S V I ♦. SMHC OJB S V I

. SMDE	S V I dim=3
		number of equations neq number of terms stored in the half-matrix n_terms block number 1
. SMHC	S V I dim=n_terms
		Line number of the th stored term
. SMDI	S V I dim=neq
		Address of the diagonal term of the th-column in the block So all the diagonal terms must be stored in the matrix.

Example:

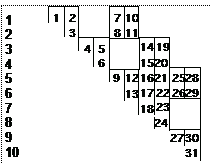
SMDI (1) = 1 SMDI (6) = 13

SMDI (2) = 3 SMDI (7) = 18

SMDI (3) = 4 SMDI (8) = 24

SMDI (4) = 6 SMDI (9) = 27

SMDI (5) = 9 SMDI (10) = 31

SMHC (1) = 1

SMHC (2) = 1

SMHC (3) = 2

SMHC (4) = 3

SMHC (5) = 3

SMHC (6) = 4

SMHC (7) = 1

SMHC (8) = 2

SMHC (9) = 5

...

SMHC (28) = 5

SMHC (29) = 6

SMHC (30) = 9

SMHC (31) = 10

6.3. Object MULT_FRONT#

For storage MULT_FRONT., the objects are as follows:

MULT_FRONT (K19): :=record

♦. ADNT OJB S V I4 ♦. GLOB OJB S V I4 ♦. LOCL OJB S V I4 ♦. PNTI OJB S V I4

Let glind be the sum of the number of neighbors of the supernodes.

♦. GLOB OJB S V I4 dim=lgind

This vector gives all the neighbors of the supernodes

♦. LOCL OJB S V I4 dim=lgind

This vector establishes, for the line numbers of the supernodes, the correspondence between the local numbering of the son and the local numbering of the father.

♦. ADNT OJB S V I4 dim=matr_init

The matr_init dimension is the size of the initial matrix (morse). It is the vector of the addresses of the initial terms in the factored matrix.

♦. PNTI OJB S V I4 dim= 19*neq+10

Cumulation of a series of work tables in the same vector.