4. Object NUME_EQUA

Object NUME_EQUA refers to the numbering of equations. It defines the numbering profile, that is, the description of unknowns. In Code_Aster, unknowns are necessarily carried by nodes. The knots in a NUME_EQUA are of two types:

• The « physical » nodes of the ma mesh (concerned by the model);

• The late knots [1] _

of one (or more) LIGRELqui rely on the ma mesh.

It contains seven objects:

NUME_EQUA (K19): :=record

♦. NEQU OJB S V I dim=2 ♦. REFN OJB S V K24 dim=5 ♦. DELG OJB S V I ♦. PRNO OJB XC V I NUM ♦. LILI OJB S N K24 ♦. NUEQ OJB S V I ♦. DEEQ OJB S V I

4.1. Item REFN

The object. REFNstocke some information:

• REFN (1): name of the mesh underlying NUME_DDL;

• REFN (2): name of the associated simple quantity (TEMP_R, DEPL_R, PRES_C,…);

• REFN (3): name of the underlying model

• REFN (4): equals” “(in the general case) or” ELIM_LAGR “

• REFN (5): value “” (in the general case) or SD name DOMJOINTS if the mesh is HPC

4.2. Item NEQU

The object. NEQUstocke the dimensions:

• NEQU (1): total number of equations (length of the. VALEdes (nodal fields);

• NEQU (2): total number of degrees of freedom (length of. NUEQ in the PROF_CHNO).

4.3. Item DELG

The object. DELGdécrit (a bit) the equations of the « Lagrange » type:

• DELG (ieq) =-1: if the equation ieq corresponds to the component LAGR carried by the second node of a mesh SEG3portant a Lagrange element (Lagrange 1);

• DELG (ieq) =-2: if the equation ieq corresponds to the component LAGR carried by the third node of a mesh SEG3portant a Lagrange element (Lagrange 2);

• DELG (ieq) =0: the equation is not of the « Lagrange » type.

4.4. Item NULG

The object. NULGest a vector for the global numbering of local degrees of freedom. It only exists in case HPC.

4.5. Item PDDL

The object. PDDLest a vector that allows you to know which processor the degrees of freedom have. It only exists in case HPC.

4.6. Item PRNO

The object. PRNO is a contiguous numbered vector collection of integers.

♦. PRNO OJB XC V I NUM

This collection describes what are the components carried by the nodes involved in PROF_CHNO by indicating the name of the LIGRELde model and those of the LIGRELà meshes and/or late knots. If it is a LIGRELà mesh and with late knots (DDL_IMPO, LIAISON_DDL…), this makes it possible to identify the late knots involved in the PROF_CHNO. On the other hand, if it is a late-knit LIGRELuniquement (FORCE_NODALE…), it does not point to any collector’s item from. PRNO.

This means that the object PRNO (1) provides information on the degrees of freedom carried by the nodes of the mesh (on which the model is necessarily based) underlying NUME_EQUA and that the other objects in the collection. PRNO (when they exist) provide information on the degrees of freedom carried by nodes that do not belong to the mesh (late nodes).

Late nodes are defined in LIGREL. For each LIGRELnomligcorrespond an object. PRNO (ili) with an II index. The LIGREL number is the number corresponding to nomligin the name pointer. LILI.

For example, the collection. PRNOcontiendra:

*. PRNO (1): nodes of the ma mesh;

*. PRNO (2): late knots of the LIGRELdont name is in. LILI (2);

*. PRNO (3): late knots of the LIGRELdont name is in. LILI (3);

*…

If NEC is the number of coded integers of the quantity associated with PROF_CHNO:

. PRNO (1) is of length (nb_knots (ma)) (2+nec);

. PRNO (1ili) is of length (nb_knots_tardifs (LIGREL (ili)) (2+nec).

Each node is described by two integers and a vector of coded integers of length neccalled the descriptor-quantity [D4.06.05 - Structure de Donnée champ].

Take the example of the nodes in the ma mesh:

• nb_cmp is the number of components carried by the inodu mesh node;

• ieq is the address in the object. NUEQde the first component carried by the ino node.

v = PRNO (1)

v (ino-1) * (2+nec) +1) = ieq

v (ino-1) * (2+nec) +2) = nb_cmp

<-.

v (ino-1) * (2+nec) +2+1) |

... | Descriptor-size of the node ino

v (ino-1) * (2+nec) +2+nec |

<-

Note:

All components carried by the same node are consecutive in . NUEQ . This is why we only store the address of the first. The components are ordered in the order of the catalog of quantities. Unfortunately, the magnitude associated with the. PRNO is not stored in the PROF_CHNO.

4.7. Item LILI

The object. LILIest a name pointer that allows access to items in the PRNO collection.

♦. LILI OJB S N K24

By convention, the value & MAILLA is stored in LILI (1), which means that the object PRNO (1) provides information on the degrees of freedom carried by the nodes of the mesh underlying the NUME_EQUA. However, the name of the mesh is not stored.

The other objects in the collection. PRNO (when they exist) provide information on the degrees of freedom carried by nodes that do not belong to the mesh (late nodes). These late nodes are defined in LIGREL. Each LIGRELnomlig corresponds to an object. PRNO (ili). The number for LIGREL is the number corresponding to nomlig in the name pointer. LILI.

4.8. Item NUEQ

The object. NUEQ is an integer vector.


♦. NUEQ OJB S V I

It is an indirection vector between the object. PRNOet the object. VALEdes CHAM_NOqui reference this NUME_EQUA. This indirection vector makes it possible to avoid the rule that the components of a node follow each other in the order of the catalog of quantities but also that each component actually corresponds to an unknown in NUME_DDL.

In practice, this vector is almost always the identity (NUEQ (I) =I). This most general case means two things:

1. There are as many unknowns in as there are components on the nodes corresponding to the LIGRELdu model and on the late nodes of the LIGRELtardifs of the dualized loads;

2. Numbering is a tautology: the unknowns are in the order of the catalog components on each node.

In the following example, we have three nodes. The first node has components DX, DYet DZ, the second node has components DXet DYet, the third node has components DXet DZ. In this case, the object. NUEQest such as NUEQ (I) =I:

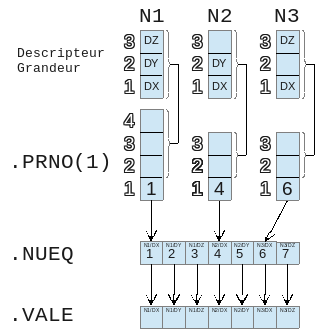
However, this vector is no longer so trivial in two specific cases:

• When creating macr_elem_stat in order to separate the internal degrees of freedom from the external degrees of freedom of the macroelement. We can then partially factor the matrices (the part corresponding to the internal ddls);

• When defining identity relationships between certain degrees of freedom. This case is used in certain situations (XFEM and contact type LAC).

For the first case, we always have. NUEQ and. VALE of the same length. On the other hand, the order is not necessarily the same. For example, we repeat the previous case by saying that node 1 must be last (it corresponds to a macroelement that must be in the last position to be able to benefit from partial factorizations in the solver LDLT). The schema becomes as follows:

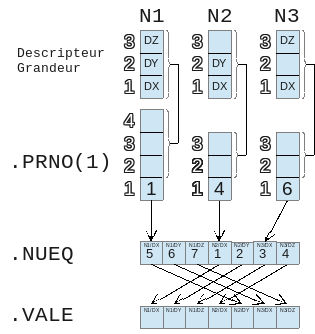
It’s always a bijection between. NUEQet. VALEmais it’s no longer a tautology (NUEQ (I) ==I). Finally, the last case is the consideration of identity relationships between two degrees of freedom. For example, we repeat the same case, except that this time, we write that the displacement DXdu second node is equal to the displacement DXdu third node.

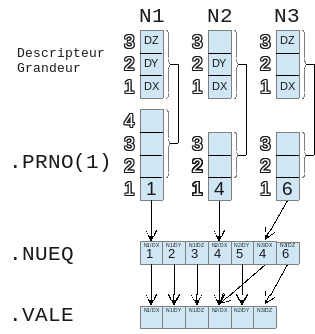
This time, we no longer have any bijections: there are fewer unknowns than degrees of freedom.

Note:

If the solver is MULT_FRONT, we check that the vector corresponds to the identity. This means that we cannot use this solver in the case of static macroelements or when there are identity relationships between degrees of freedom. In these cases, solver MUMPS should be used.

4.9. Item DEEQ

The object. DEEQ is an integer vector of length 2*neq. With neq is the number of equations in NUME_EQUA.

 ♦. DEEQ OJB S V I DIM =2*neq

It is an « inverse » vector of. PRNOqui describes (partially) the equations.

If nueq is an equation number (i.e. address in the object). VALE), so:

V (nueq-1) *2+1): ino

V (nueq-1) *2+2): icmp

With the following convention:

• If ino>0 and icmp>0: neqis the equation associated with the fifth component carried by the inode mesh node.

• If ino>0 and icmp<0: nueq is one of the two equations that dualize the blocking of the icmpth component of the ino node of the mesh.

• If ino=0 and icmp=0: nueq is an equation for dualizing a linear relationship between several components.

Note:

In the case of taking identity relationships into account in the numbering, as several nodes/components correspond to the same equation, by convention, the first node/component pair is indicated.

[1]

A late node in Code_Aster corresponds to a node added by a dualized boundary condition (DDL_IMPO, LIAISON_DDL,…). This node was added when the load was created and stored in the corresponding LIGREL to carry the Lagranges. They do not appear in the mesh data structure and have negative numbers.