3. Modeling A#

3.1. Characteristics of modeling#

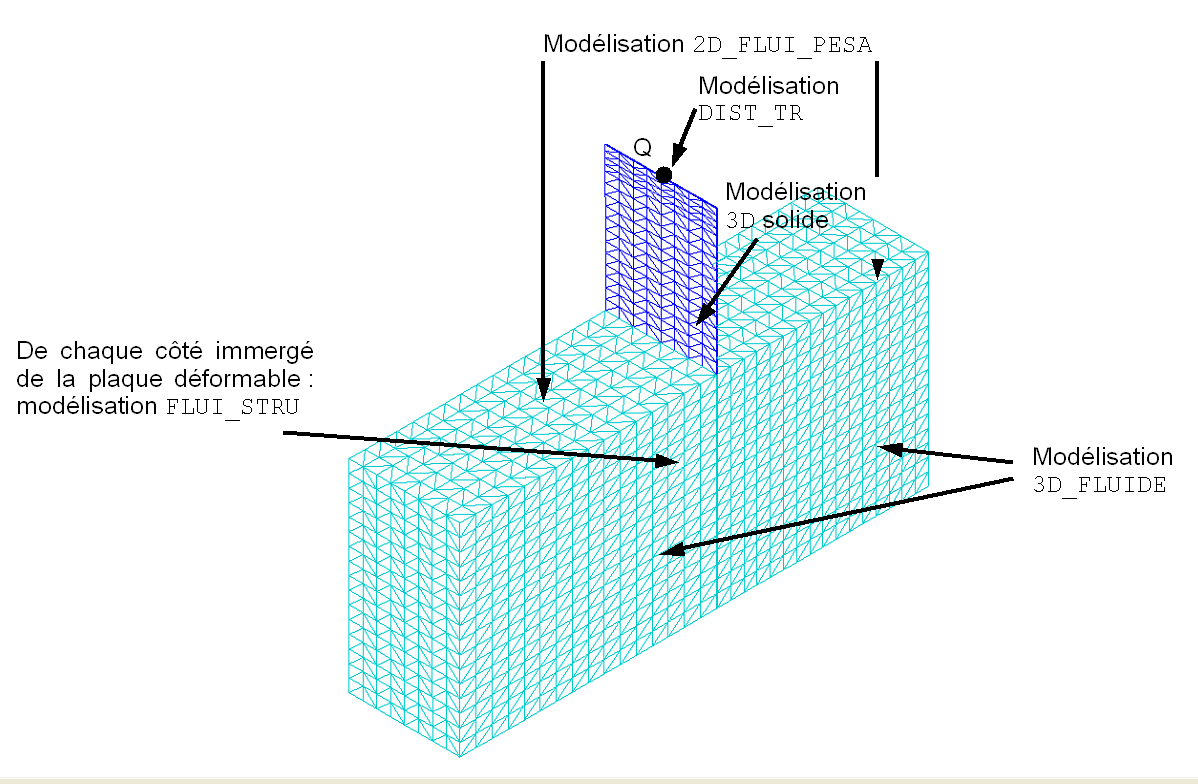
_images/10000000000004AE0000031090491E2344399B1A.png

  1. The total mesh includes 8163 knots, i.e. approximately 125,000 degrees of freedom,

  2. The point element \(Q\) (modeling DIS_TR) makes it possible to simply represent an accelerometer present in the model in article [bib1],

  3. The deformable plate is modelled by 5120 solid solid elements (3D modeling) pentahedral with 6 knots (10 layers in the thickness for a good approximation of the flexural behavior despite the linearity of the elements),

  4. the free surface is modelled by 512 elements MEFP_FACE3 (2D_ FLUI_PESA modeling) triangles with 3 knots,

  5. the fluid volume is modeled by 24576 fluid elements (3D modeling FLUIDE) tetrahedral fluid elements with 4 nodes.

3.2. Writing boundary conditions#

The bottom of the tank can only move in direction \(x\):

DDL_IMPO =( _F ( GROUP_NO =( “FONDS”, “FONDP”,), DY=0.0, DZ=0.0,),),);

In this direction \(x\), a sinusoidal displacement in time, with a frequency \(\mathrm{1,7704}\mathrm{Hz}\) and an amplitude \(\mathrm{0,001}m\), is imposed on the bottom of the tank:

LFONC = DEFI_LIST_REEL (DEBUT =0.0, INTERVALLE =_F (JUSQU_A =10.0, PAS =0.01,),); FONC = FORMULE (REEL = « ”(REEL: INST) = (0.001) SIN (2*PI*FREQ INST) « ”); DEPLX = CALC_FONC_INTERP (FONCTION = FONC, NOM_PARA =” INST “, LIST_PARA = LFONC,); CHARG_SE = AFFE_CHAR_MECA_F (MODELE = MODELE, DDL_IMPO =_F ( GROUP_NO =( “FONDS”, “FONDP”,), DX= DEPLX,),);

Volume gravity loading is defined as follows:

PESA = AFFE_CHAR_MECA (MODELE = MODELE,

PESANTEUR =_F (GRAVITE =9.81, DIRECTION =( 0.,0., -1.,),),);

3.3. Characteristics of the mesh#

The mesh contains:

24575 TETRA4

5120 PENTA6

4096 TRIA3

3.4. Tested values#

The tests are carried out on the value of the following displacement \(x\) (noted \(\mathit{DX}\)) for various times and for the nodes \(\mathit{N145}\) and \(\mathit{N3119}\).

Identification

Reference

\(\mathit{DX}(\mathit{N145},t=\mathrm{0,8}s)\)

5.162416932321991e-04

\(\mathrm{DX}(\mathrm{N145},t=\mathrm{1,4}s)\)

1.4970110110314375e-04

\(\mathrm{DX}(\mathrm{N145},t=\mathrm{2,0}s)\)

-2.392741313131721e-04

\(\mathrm{DX}(\mathrm{N3119},t=\mathrm{1,0}s)\)

-9.973627272860105e-04

\(\mathrm{DX}(\mathrm{N3119},t=\mathrm{1,6}s)\)

-8.785505656121762e-04

\(\mathrm{DX}(\mathrm{N3119},t=\mathrm{2,0}s)\)

-2.392916161952584e-04

We also test the critical eigenvalue calculated with CRIT_STAB.

Identification

Reference

CHAR_CRIT

-2.477264942149