1. Reference problem#
1.1. Geometry#
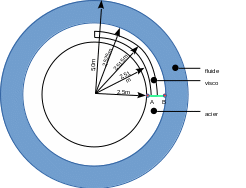
Figure 1.1-1: Geometry (not scaled) We consider a flat metal ring immersed in a fluid medium with an external border for the latter (figure).
In the metal ring, a visco-elastic layer is modeled over a quarter of the circumference.
1.2. Material properties#
For the steel part, an isotropic elastic material is considered:
Modulus of elasticity: \({E}_{a}=177\mathit{GPa}\)
Poisson’s ratio: \({\mathrm{\nu }}_{a}=0.3\)
Density: \({\mathrm{\rho }}_{a}=7450\mathit{kg}\mathrm{.}{m}^{-3}\)
For the fluid, it is water with the following characteristics:
Speed of sound: \(c=1500m\mathrm{.}{s}^{-1}\)
Density: \({\mathrm{\rho }}_{e}=1000\mathit{kg}\mathrm{.}{m}^{-3}\)
For the visco-elastic part, we consider a material of the fractional derivative model type (Zener model) whose shear modulus depends on the pulsation:
The characteristics are as follows:
Poisson’s ratio: \({\mathrm{\nu }}_{v}=0.49\) (almost incompressible material)
Density: \({\mathrm{\rho }}_{v}=1460\mathit{kg}\mathrm{.}{m}^{-3}\)
Coefficient: \({G}_{0}=\mathrm{2,11}\mathit{MPa}\), \({G}_{\mathrm{\infty }}=\mathrm{0,59}\mathit{GPa}\), \(\mathrm{\tau }=\mathrm{0,44}\times {10}^{-6}\), and \(\mathrm{\alpha }=\mathrm{0,53}\)
Note: to improve the calculation of the modes, all these quantities are a-dimensioned in relation to water.
1.3. Boundary conditions and loads#
For the structure part, an embedment condition is imposed on the segment \(\mathit{AB}\) and a horizontal nodal force \(\mathit{Fx}=A\mathrm{,0}\times {10}^{-5}N\) is imposed on the point \(A\).
A fluid-boundary interaction condition is achieved by the use of 2D_ FLUI_STRU elements at the interface between the structure and the fluid. Moreover, an impedance condition is defined on the external border of the fluid, by a loading of type IMPE and the calculation of the impedance matrices that are linked to it.