1. Reference problem

1.1. Geometry

1.2. Material properties

The material obeys Norton’s law of viscoplastic behavior (particular case of Lemaître’s law, where the parameter UN_SUR_M is zero, confer [R5.03.08]), whose parameters are:

Young’s module: \(E\mathrm{=}80000\mathit{MPa}\)

Poisson’s ratio: \(\nu \mathrm{=}0.35\)

\(n\mathrm{=}4.39\)

\(K\mathrm{=}\frac{1}{0.003944}{\mathit{MPa.s}}^{\text{-1}}\)

1.3. Boundary conditions and loads

The bar, of initial length \({I}_{0}\), locked in the direction \(\mathrm{Ox}\) on the face on the face \([\mathrm{1,}2]\), is subjected to a uniform temperature \(T\) and to a mechanical tensile movement \({u}^{\mathit{meca}}\) on the face \([\mathrm{3,}4]\). The loading sequences are as follows:

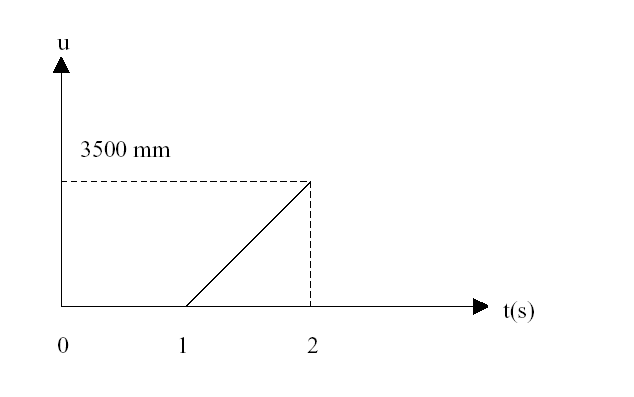
Reference temperature: \({T}_{\mathrm{réf}}=700°C\).

Note:

The uniform temperature imposed on the element, constant over time and equal to the reference temperature, is only used to operate the model META_LEMA_ANI . There is no thermal expansion.