1. Reference problem#
1.1. Device description#
The non-linear element is represented by the rheological model below.

Figure a : Device model.
Length of SEG2: \(L=0.1m\)
The equations governing behavior are in [R5.03.17].
1.2. Modeling#
The modeling tested is on an element DIS_T, mesh SEG2. The characteristic of the discrete element is of the type: K_T_D_L.
Note: The units of the parameters must agree with the unit of effort, the unit of lengths [R5.03.17]. For all models the units are homogeneous to [N], [m].
1.2.1. A, B models#
These models make it possible to test the non-linear static cyclic behavior of the law.
1.3. Material properties#
1.3.1. Modeling A#
The properties are:
the non-linear function [R5.03.17].
the values of dist1 and dist2. For this modeling, they are zero.
The table shows the x-axis and ordinate values of the function.
X [m] |
0.00 |
0.200 |
0.200 |
0.500 |
0.700 |
0.950 |
1.000 |
Force [N] |
0.00 |
400.0 |
400.0 |
450.0 |
600.0 |
700.0 |
1000.0 |
Table a :: ** Abscissa and ordinates of the function.
The function is extended linearly to the right.
The figure shows the non-linear behavior used in the test case.
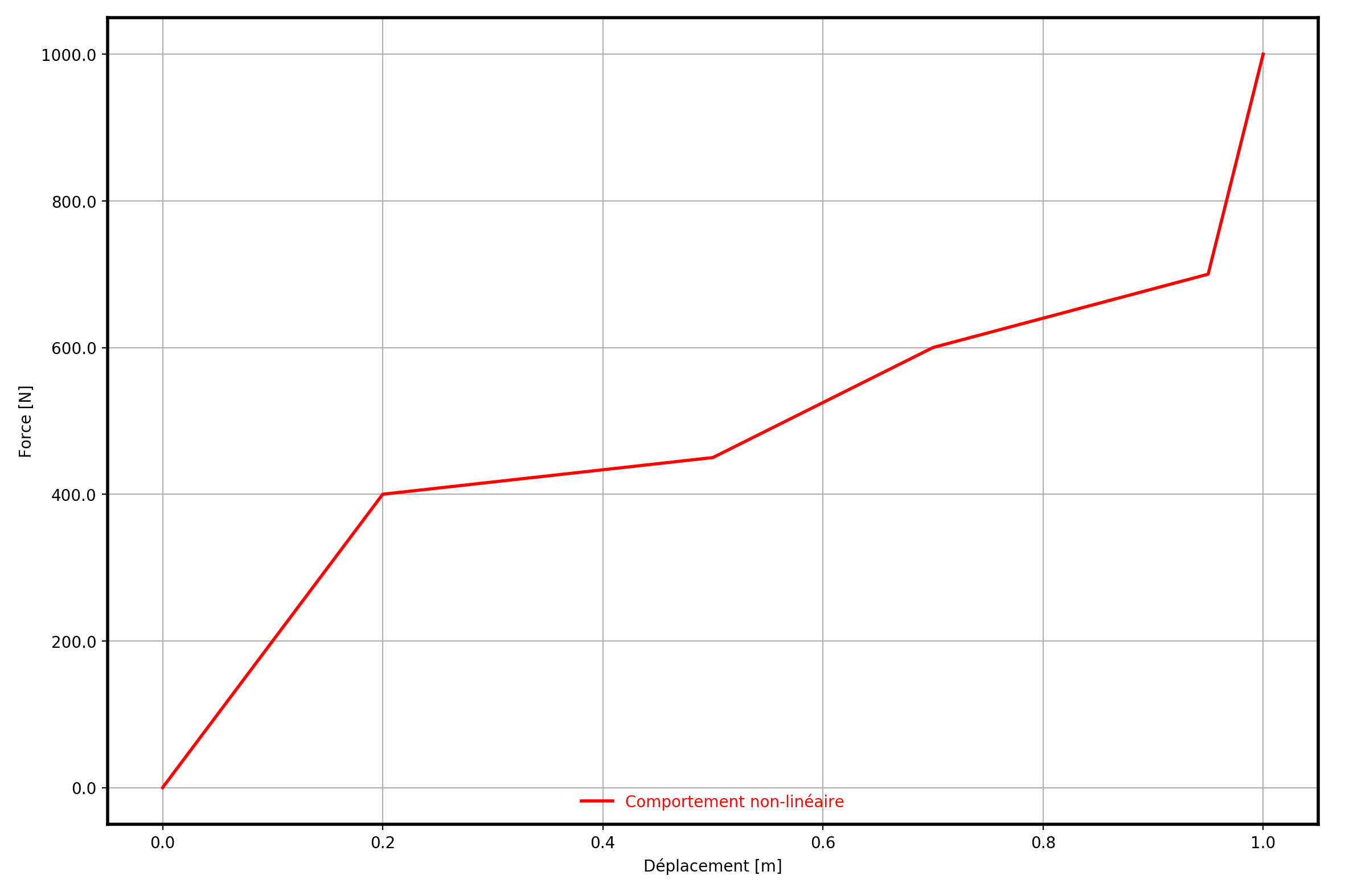
Figure b : Nonlinear behavior.
1.3.2. B modeling#
The properties are:
the non-linear function [R5.03.17]. Same as modeling « a ».
the values of dist1 and dist2. For this modeling \(\text{DIST1}=0.50\ast L\), \(\text{DIST2}=0.25\ast L\)
1.4. Boundary conditions and loads#
1.4.1. A, B models#
The discrete is a SEG2, the node N2 is blocked, on the node N1 the movement condition is imposed.
The moving condition is a function of time, longSeg2 is the length of SEG2.
INST |
DX |
0.0 |
0.0*longseg2 |
1.0 |
0.8*longseg2 |
2.0 |
2.0*Longseg2 |
3.0 |
4.0* LongSeg2 |
3.5 |
3.0*longseg2 |
5.0 |
0.0*longseg2 |
8.0 |
3.0*longseg2 |
10.0 |
15.0*longseg2 |
20.0 |
0.0*longseg2 |
Table b : Load function.