5. C modeling#

5.1. Characteristics of modeling#

We take advantage of the symmetries of the problem to model only one eighth of the sphere.

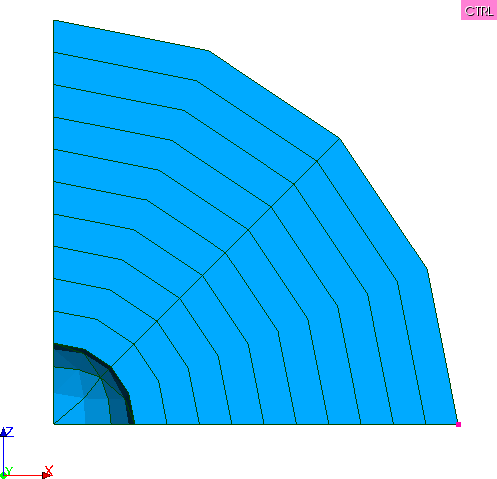
Three models are tested: 3D_ INCO_UPG (SIMO_MIEHE and GDEF_LOG) and 3D_ INCO_UP

5.2. Characteristics of the mesh#

The 279 node mesh contains 60 PENTA15 elements.

5.3. Tested sizes and results#

The stress trace and the cumulative plastic deformation are tested for the most eccentric and the least eccentric Gauss points.

MODELISATION =”3D_ INCO_UPG “and DEFORMATION =” SIMO_MIEHE”

Identification	Reference type	Reference value	Tolerance
Least offset Gauss point - \(\mathit{tr}\sigma\) - Pa	“ANALYTIQUE”	-1069165300.4	1%
Outermost Gauss point - \(\mathit{tr}\sigma\) - Pa	“ANALYTIQUE”	293654077.71	1%
Least offset Gauss point - \(p\)	“ANALYTIQUE”	0.1205244945	17%
Outermost Gauss point - \(p\)	“ANALYTIQUE”	2.1945807187e-5	1E -5%

MODELISATION =”3D_ INCO_UPG “and DEFORMATION =” GDEF_LOG”

Identification	Reference type	Reference value	Tolerance
Least offset Gauss point - \(\mathit{tr}\sigma\) - Pa	“ANALYTIQUE”	-1069097464.2	1%
Outermost Gauss point - \(\mathit{tr}\sigma\) - Pa	“ANALYTIQUE”	293654247.5	1%
Least offset Gauss point - \(p\)	“ANALYTIQUE”	0.12049702407	17%
Outermost Gauss point - \(p\)	“ANALYTIQUE”	2.1945190693e-5	1E -5%

MODELISATION =”3D_ INCO_UP “and DEFORMATION =” GDEF_LOG”

Identification	Reference type	Reference value	Tolerance
Least offset Gauss point - \(\mathit{tr}\sigma\) - Pa	“ANALYTIQUE”	-1069097462.2	1%
Outermost Gauss point - \(\mathit{tr}\sigma\) - Pa	“ANALYTIQUE”	293654247.46	1%
Least offset Gauss point - \(p\)	“ANALYTIQUE”	0.12049702379	17%
Outermost Gauss point - \(p\)	“ANALYTIQUE”	2.1945190811e-5	1E -5%

5.4. notes#

All incompressible formulations give good results. It can be seen from the that there are no more oscillations in the value of the stress trace with incompressible formulations unlike standard 3D elements.

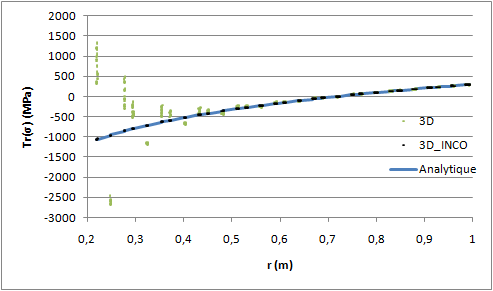
Figure 5.4-a : Trace the constraints in \(\mathit{Mpa}\) for the formulations 3D , 3D_ INCO and the analytical solution